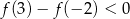Zestaw użytkownika nr 6696_7673
sprawdzian l LO poprawawłasności funkcjiCzas pracy: 45 min.Suma punktów: 28
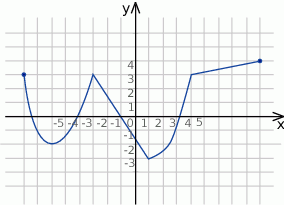
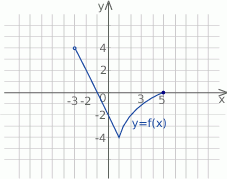
Na poniższym rysunku przedstawiono łamaną  , która jest wykresem funkcji
, która jest wykresem funkcji 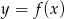 .
.
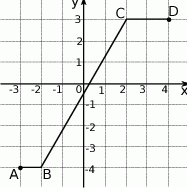
Korzystając z tego wykresu
- zapisz w postaci przedziału zbiór wartości funkcji
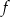 ,
, - podaj wartość funkcji
 dla argumentu
dla argumentu 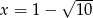 ,
, - wyznacz równanie prostej
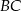 ,
, - oblicz długość odcinka
 .
.
Z danego wykresu funkcji 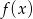 odczytaj
odczytaj
- zbiór wartości funkcji
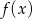 ;
; - rozwiązania równania
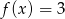 ;
; - maksymalne przedziały monotoniczności funkcji
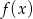 .
.
Na rysunku poniżej przedstawiony jest wykres funkcji 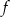 , określonej w przedziale
, określonej w przedziale 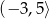 .
.
- Podaj maksymalne przedziały monotoniczności funkcji
 .
. - Naszkicuj w tym samym układzie współrzędnych wykres funkcji
 , opisanej wzorem
, opisanej wzorem 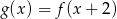 .
. - Wyznacz zbiór wszystkich argumentów należących do przedziału
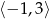 , dla których wartości funkcji
, dla których wartości funkcji 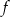 są większe niż wartości funkcji
są większe niż wartości funkcji 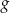 .
.
Na rysunku jest przedstawiony wykres funkcji 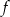 .
.
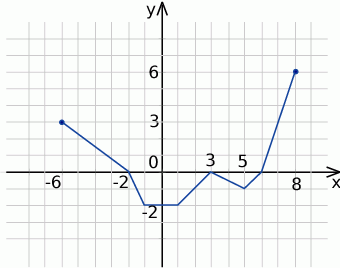
- Podaj dziedzinę funkcji
 .
. - Podaj wszystkie miejsca zerowe funkcji
 .
. - Odczytaj wartość funkcji
 dla argumentu
dla argumentu 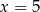 .
. - Podaj zbiór wartości funkcji
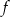 .
. - Podaj maksymalny przedział o długości 3, w którym funkcja
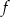 jest rosnąca.
jest rosnąca. - Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja
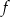 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Funkcja 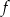 określona jest wzorem
określona jest wzorem
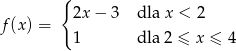
- Uzupełnij tabelę:
x -3 3 f(x) 0 - Narysuj wykres funkcji
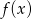 .
. - Podaj liczby całkowite
 , spełniające nierówność
, spełniające nierówność 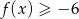 .
.
Zbiór wartości funkcji kwadratowej 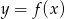 jest rozłączny z przedziałem
jest rozłączny z przedziałem 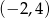 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 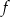 ?
?
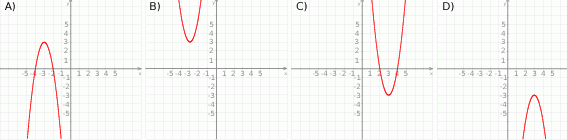
Rysunek przedstawia wykres funkcji 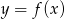 .
.
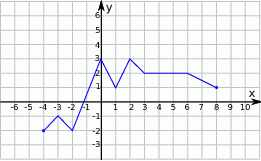
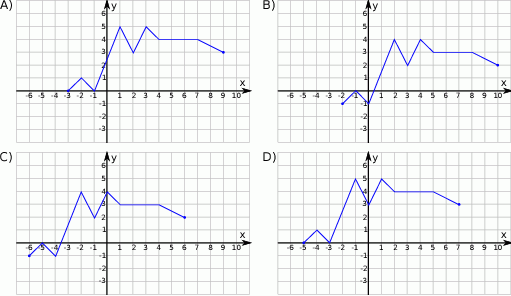
Wskaż wykres funkcji 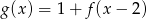 .
.
Aby na podstawie wykresu funkcji 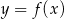 narysować wykres funkcji
narysować wykres funkcji 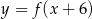 , należy wykres funkcji
, należy wykres funkcji  przesunąć o
przesunąć o
A) 6 jednostek do dołu
B) 6 jednostek w prawo
C) 6 jednostek do góry
D) 6 jednostek w lewo
Rysunek przedstawia wykres funkcji  .
.
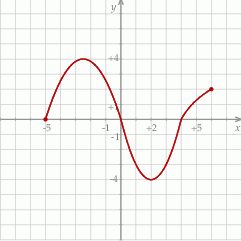
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 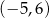
B) 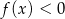 dla
dla 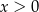
C) funkcja ma dwa miejsca zerowe
D) zbiór wartości funkcji to 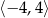
Na rysunku przedstawiony jest wykres funkcji 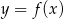 . Dziedziną funkcji
. Dziedziną funkcji 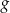 , gdzie
, gdzie 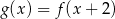 jest zbiór
jest zbiór
A)  B)
B)  C)
C)  D)
D) 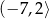
Do wykresu funkcji 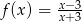 należy punkt
należy punkt
A) 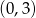 B)
B) 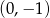 C)
C) 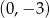 D)
D) 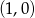
Dziedziną funkcji 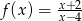 jest zbiór:
jest zbiór:
A) 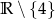 B)
B) 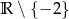 C)
C) 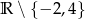 D)
D) 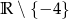
Dana jest funkcja
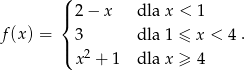
Wówczas
A) 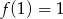 B)
B) 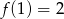 C)
C) 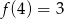 D)
D) 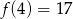
Funkcja 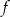 określona jest wzorem
określona jest wzorem
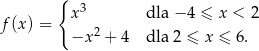
Prawdziwa jest nierówność
A) 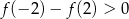
B) 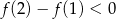
C) 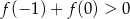
D)