Zestaw użytkownika nr 6718_4084
Planimetria - Trójkąty (2)zdania łatwe
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 6 B) 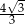 C)
C) 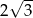 D)
D) 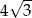
Pole trójkąta o bokach 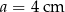 i
i 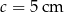 oraz kącie
oraz kącie 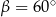 zawartym między danymi bokami jest równe
zawartym między danymi bokami jest równe
A) 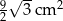 B)
B) 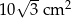 C)
C) 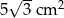 D)
D) 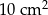
W trójkącie jeden z kątów jest o 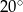 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 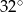 B)
B) 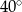 C)
C) 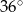 D)
D) 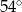
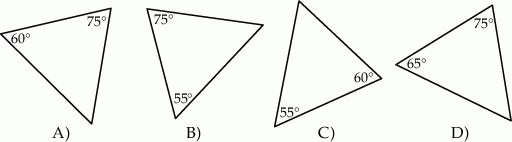
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 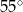 i
i 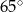 ?
?
Środkiem okręgu opisanego na trójkącie jest punkt przecięcia się
A) dwusiecznych kątów trójkąta
B) wysokości trójkąta
C) środkowych trójkąta
D) symetralnych boków trójkąta
Nie jest prawdziwe zdanie
A) Środkowe trójkąta dzielą się w stosunku 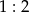 .
.
B) Środek ciężkości trójkąta to punkt przecięcia się wysokości trójkąta.
C) Środek okręgu opisanego na trójkącie to punkt przecięcia się symetralnych boków trójkąta.
D) Środek okręgu wpisanego w trójkąt to punkt przecięcia się dwusiecznych kątów trójkąta.
Liczby 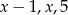 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku tego trójkąta.
Punkt 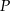 jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 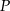 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 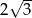 ?
?
Liczby 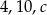 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 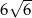 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
Oblicz pole trójkąta równoramiennego, w którym odległość wierzchołka kąta prostego od przeciwprostokątnej jest równa 5 cm.
W trójkącie równoramiennym 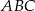 , w którym
, w którym 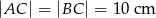 , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 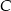 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
W trójkącie równoramiennym podstawa ma długość 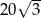 . Pole trójkąta jest równe
. Pole trójkąta jest równe 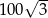 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
. Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
Liczby 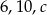 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Podstawa trójkąta równoramiennego ma miarę 4 cm, a kąt przy niej 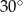 . Oblicz pole i obwód trójkąta.
. Oblicz pole i obwód trójkąta.
Oblicz pole trójkąta równoramiennego 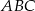 , w którym
, w którym 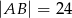 i
i 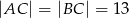 .
.
Ostrokątny trójkąt równoramienny 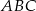 o podstawie
o podstawie 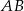 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 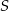 , przy czym kąt
, przy czym kąt 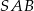 ma miarę
ma miarę 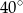 . Oblicz miarę kąta
. Oblicz miarę kąta 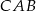 .
.
Jaki warunek musi spełniać liczba  , aby istniał trójkąt o bokach
, aby istniał trójkąt o bokach 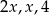 ?
?
Dany jest trójkąt o wymiarach 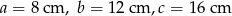 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
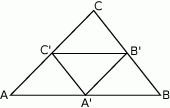
Punkty 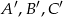 są środkami boków trójkąta
są środkami boków trójkąta 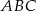 . Pole trójkąta
. Pole trójkąta 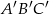 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 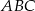 .
.
Miary dwóch kątów trójkąta wynoszą 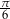 i
i 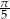 . Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
. Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Dane są miary łukowe dwóch kątów trójkąta: 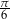 i
i 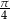 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.
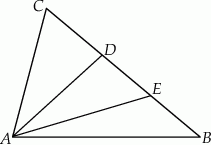
Punkty 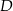 i
i 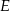 dzielą bok
dzielą bok 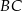 trójkąta
trójkąta 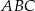 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 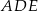 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta 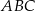 .
.
Dane są dwa boki trójkąta: 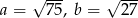 . Jaką długość może przyjmować trzeci bok trójkąta?
. Jaką długość może przyjmować trzeci bok trójkąta?
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.
W trójkącie ostrokątnym 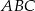 , którego pole równa się 16, boki
, którego pole równa się 16, boki 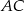 i
i 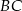 mają długości
mają długości 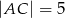 ,
, 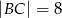 . Oblicz długość boku
. Oblicz długość boku 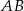 .
.
Wysokość 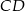 trójkąta
trójkąta 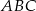 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 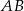 na odcinki o długościach
na odcinki o długościach 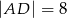 i
i 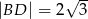 .
.
- Oblicz tangens i cosinus kąta
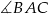 .
. - Znajdź miarę kąta
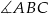 .
.
Wysokość 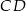 trójkąta
trójkąta 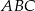 tworzy z bokami
tworzy z bokami 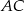 i
i 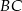 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 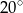 i
i 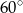 . Punkt
. Punkt 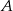 należy do odcinka
należy do odcinka 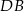 .
.
- Narysuj trójkąt
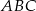 i jego wysokość
i jego wysokość 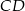 .
. - Wyznacz miary kątów trójkąta
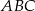 .
.
Dany jest trójkąt o bokach długości 4 (podstawa trójkąta), 5 i 6 – boki trójkąta. Przez punkt przecięcia się środkowych trójkąta prowadzimy prostą równoległą do podstawy. Oblicz obwód trójkąta którego podstawą jest ta prosta.

