Zestaw użytkownika nr 6743_7023
Zestaw użytkownika
nr 6743_7023
Na rysunku przedstawiony jest wykres funkcji 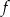 określonej wzorem
określonej wzorem 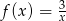 dla
dla 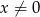 .
.
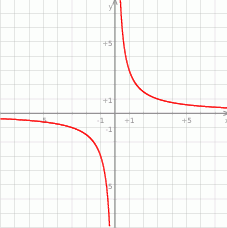
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 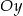 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 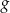 o wzorze
o wzorze 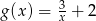 dla
dla 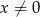 .
.
- Narysuj wykres funkcji
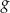 .
. - Oblicz największą wartość funkcji
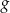 w przedziale
w przedziale 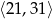 .
. - Podaj, o ile jednostek wzdłuż osi
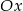 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 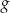 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Dana jest funkcja 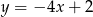 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ v = [2,0]](https://img.zadania.info/zad/9122741/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 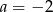 , której wykres przecina oś
, której wykres przecina oś 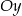 w punkcie
w punkcie 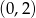 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Wyznacz współczynniki  i
i 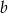 funkcji kwadratowej
funkcji kwadratowej 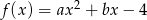 , jeśli współrzędne wierzchołka wynoszą
, jeśli współrzędne wierzchołka wynoszą 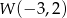 . Przedstaw trójmian w postaci iloczynowej.
. Przedstaw trójmian w postaci iloczynowej.
Dana jest funkcja 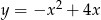 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→ u = [− 2,3]](https://img.zadania.info/zad/9470655/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Funkcja 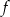 określona jest wzorem
określona jest wzorem 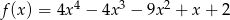 .
.
- Znajdź punkt przecięcia wykresu funkcji
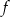 z osia
z osia 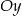 .
. - Znajdź, o ile istnieją, punkty przecięcia funkcji
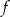 z osia
z osia 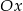 .
. - Wyznacz te argumenty, dla których funkcje
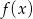 i funkcja
i funkcja 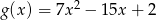 przyjmują tę samą wartość.
przyjmują tę samą wartość.
Funkcja 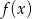 , gdzie
, gdzie 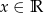 dana jest wzorem
dana jest wzorem
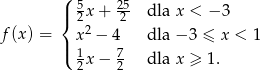
- Narysuj wykres funkcji
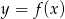 .
. - Odczytaj z wykresu rozwiązanie nierówności
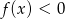 .
.
Napisz wzór funkcji liniowej, której wykres jest równoległy do wykresu funkcji 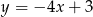 i przecina oś
i przecina oś 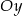 w punkcie
w punkcie 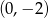 .
.
Dany jest wykres funkcji 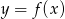 określonej dla
określonej dla 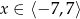 .
.
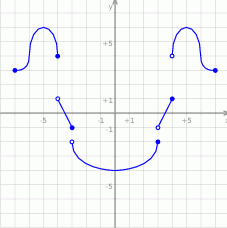
Odczytaj z wykresu:
- rozwiązania równania
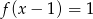 ;
; - miejsca zerowe funkcji
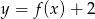 ;
; - maksymalne przedziały monotoniczności funkcji
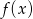 .
.

