Zestaw użytkownika nr 6745_6317
Zestaw użytkownika
nr 6745_6317
Na bokach 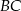 i
i 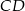 równoległoboku
równoległoboku 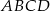 zbudowano kwadraty
zbudowano kwadraty 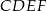 i
i  (zobacz rysunek).
(zobacz rysunek).
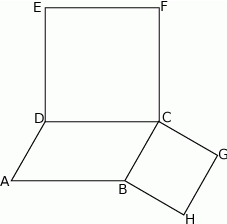
Udowodnij, że 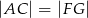 .
.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
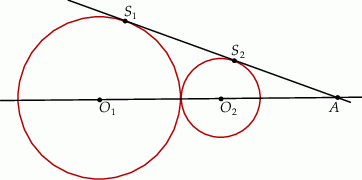
Dane są 2 koła styczne zewnętrznie o promieniach 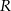 i
i  (
(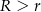 ) oraz środkach
) oraz środkach 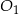 i
i 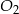 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 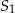 i
i 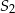 odpowiednio (
odpowiednio (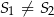 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 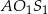 , gdzie
, gdzie 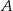 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 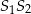 i
i 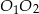 .
.
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
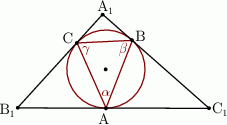
Boki trójkąta 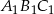 są styczne do okręgu w punktach
są styczne do okręgu w punktach 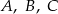 , a kąty trójkąta
, a kąty trójkąta 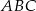 są odpowiednio równe
są odpowiednio równe 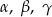 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 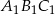 .
.
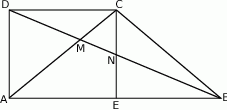
Punkt 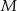 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 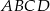 . Punkt
. Punkt 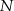 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 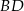 i wysokości
i wysokości 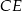 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 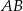 . Wykaż, że
. Wykaż, że 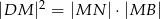 .
.
Na zewnątrz kwadratu 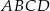 na bokach
na bokach 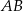 i
i 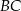 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 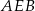 i
i 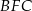 . Uzasadnij, że proste
. Uzasadnij, że proste 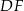 i
i 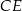 są prostopadłe.
są prostopadłe.
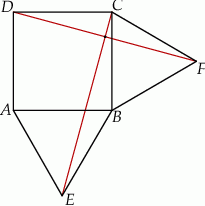
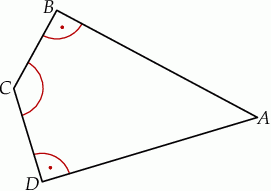
W czworokącie wypukłym 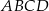 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 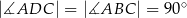 oraz
oraz 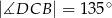 . Wykaż, że
. Wykaż, że 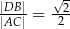 .
.
Oblicz sinusy kątów ostrych trójkąta prostokątnego, wiedząc, że stosunek długości promienia okręgu wpisanego do promienia okręgu opisanego na tym trójkącie jest równy 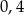 .
.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 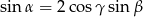 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
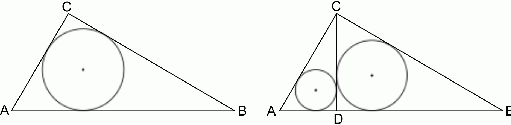
Dany jest trójkąt prostokątny 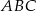 , w którym
, w którym 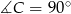 . W trójkącie tym poprowadzono wysokość
. W trójkącie tym poprowadzono wysokość 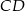 . Wykaż, że
. Wykaż, że 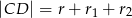 , gdzie
, gdzie 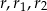 są odpowiednio długościami promieni okręgów wpisanych w trójkąty
są odpowiednio długościami promieni okręgów wpisanych w trójkąty 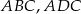 i
i 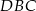 .
.
W trapezie 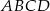 boki nierównoległe
boki nierównoległe 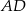 i
i 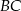 zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane
zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane 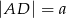 oraz
oraz 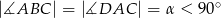 .
.

