Zestaw użytkownika nr 6755_3718

Zestaw użytkownika
nr 6755_3718

Zadanie 1

(5 pkt)

Promień i wysokość walca mają jednakową długość. Pole powierzchni bocznej wynosi 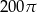200 π . Oblicz pole podstawy walca.

Zadanie 2

(5 pkt)

Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 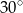30 ∘ .

Zadanie 3

(5 pkt)

Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.

Zadanie 4

(5 pkt)

Trapez prostokątny obraca się wokół boku tworzącego z podstawami kąty proste. Podstawy trapezu mają długość odpowiednio 10 i 7. Pole trapezu wynosi 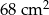68cm 2 . Oblicz objętość otrzymanej bryły.

Zadanie 5

(5 pkt)

Ołowianą kulę o średnicy 60 cm przetopiono na walce o wysokości i promieniu podstawy równych 2 cm. Ile takich walców otrzymano?

Zadanie 6

(5 pkt)

Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 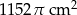2 1152π cm .

Zadanie 7

(5 pkt)

Objętość stożka jest równa 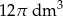3 12π dm , a cosinus kąta między wysokością, a tworzącą wynosi 0,8. Oblicz:

pole powierzchni bocznej stożka;
miarę kąta środkowego powierzchni bocznej stożka po rozwinięciu na płaszczyźnie.

Zadanie 8

(5 pkt)

Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 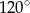120∘ (zobacz rysunek). Oblicz objętość tego stożka.

Zadanie 9

(5 pkt)

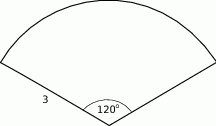
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.

Zadanie 10

(5 pkt)

Pole powierzchni bocznej stożka jest czterokrotnie większe od pola podstawy stożka. Oblicz wysokość stożka, wiedząc, że promień jego podstawy jest równy .

Arkusz Wersja PDF