Zestaw użytkownika nr 6840_7511
podstawa styczeń 2012
Jeżeli 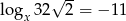 to liczba
to liczba  jest równa
jest równa
A) 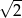 B)
B) 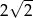 C) 2 D)
C) 2 D) 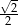
Wiadomo, że 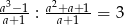 . Zatem
. Zatem 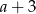 jest równe
jest równe
A) 1 B) 7 C) 5 D) -1
Zbiorem wszystkich rozwiązań równania 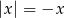 jest
jest
A) 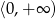 B)
B) 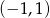 C)
C) 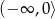 D)
D) 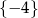
Wyrażenie 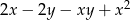 jest równe wyrażeniu
jest równe wyrażeniu
A) 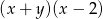 B)
B) 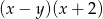 C)
C) 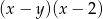 D)
D) 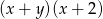
Ile liczb wymiernych znajduje się w zbiorze
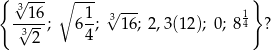
A) 5 B) 3 C) 2 D) 4
Wśród liczb naturalnych należących do przedziału (31, 41)
A) jest jedna liczba pierwsza
B) są trzy liczby pierwsze
C) są dwie liczby pierwsze
D) nie ma liczb pierwszych
Wskaż prawdziwą równość
A) 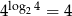 B)
B) 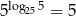 C)
C) 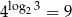 D)
D) 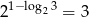
Liczbę 6,49 zaokrąglamy do najbliższej liczby całkowitej. Błąd względny tego przybliżenia z dokładnością do 0,1% jest równy
A) 7,5% B) 8% C) 4,7% D) 7,6%
Suma  początkowych liczb naturalnych dodatnich nieparzystych jest równa
początkowych liczb naturalnych dodatnich nieparzystych jest równa
A) 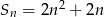 B)
B) 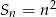 C)
C) 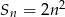 D)
D) 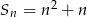
Osią symetrii paraboli będącej wykresem funkcji 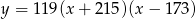 jest prosta o równaniu
jest prosta o równaniu
A) 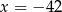 B)
B) 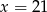 C)
C) 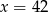 D)
D) 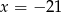
Wierzchołek paraboli 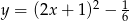 leży na prostej o równaniu
leży na prostej o równaniu
A) 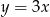 B)
B) 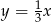 C)
C) 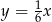 D)
D) 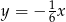
Przesuwając wykres funkcji 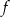 wzdłuż osi
wzdłuż osi 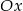 o 6 jednostek w prawo, otrzymano wykres funkcji
o 6 jednostek w prawo, otrzymano wykres funkcji 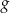 . Zatem
. Zatem
A) 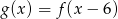 B)
B) 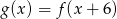 C)
C) 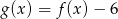 D)
D) 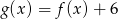
Wykres funkcji 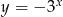 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) III i IV B) II i III C) I i II D) IV i I
Dziedziną funkcji 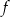 jest przedział
jest przedział 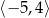 . Obok zamieszczono wykres tej funkcji.
. Obok zamieszczono wykres tej funkcji.
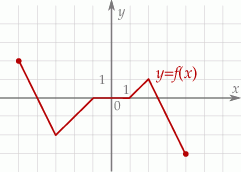
Funkcja 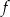 jest malejąca w zbiorze
jest malejąca w zbiorze
A) 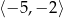 B)
B) 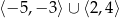 C)
C) 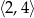 D)
D) 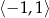
Układ równań 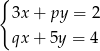 z niewiadomymi
z niewiadomymi  i
i 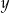 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 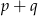 jest równa
jest równa
A) 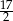 B) 15 C) 6 D)
B) 15 C) 6 D) 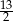
Iloczyn pierwiastków równania 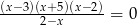 jest równy
jest równy
A) 30 B) -30 C) 15 D) -15
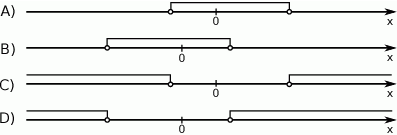
Zbiór rozwiązań nierówności 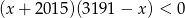 może być przedstawiony na rysunku
może być przedstawiony na rysunku
Zbiorem rozwiązań nierówności 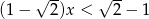 jest przedział
jest przedział
A) 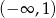 B)
B) 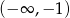 C)
C) 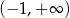 D)
D) 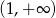
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 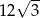 B)
B)  C)
C) 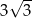 D)
D) 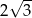
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna tego trójkąta ma długość
A) 14 B) 18 C) 20 D) 24
Odcinek 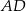 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 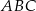 poprowadzoną do ramienia
poprowadzoną do ramienia 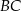 .
.
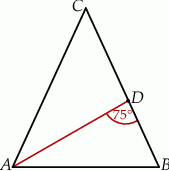
Jeżeli 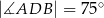 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 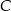 jest równa
jest równa
A) 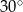 B)
B) 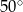 C)
C) 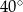 D)
D) 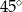
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 70 B) 28 C) 280 D) 21
Wybieramy jedną liczbę ze zbioru 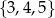 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 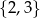 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 4 C) 5 D) 3
Średnia arytmetyczna wszystkich liczb pierwszych należących do przedziału 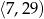 jest równa
jest równa
A) 16,6 B) 18,6 C) 15 D) 17
Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów pewnej klasy.
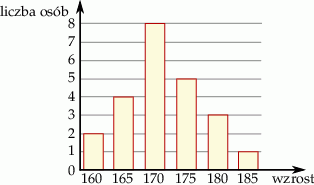
Ile osób w tej klasie ma wzrost powyżej średniego?
A) 17 B) 9 C) 4 D) 21
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Uprość wyrażenie
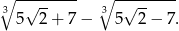
Wykaż, że jeżeli 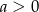 i
i 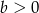 oraz
oraz 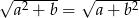 , to
, to 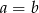 lub
lub 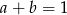 .
.
Wyznacz wzór funkcji liniowej 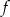 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 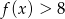 jest przedział
jest przedział 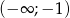 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 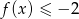 jest przedział
jest przedział 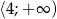 .
.
Funkcja homograficzna 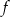 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 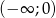 i
i 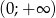 . Zbiór
. Zbiór 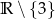 jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
- Znajdź wzór funkcji
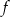 .
. - Wyznacz miejsce zerowe funkcji
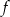 .
. - Wyznacz te argumenty, dla których funkcja
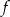 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Uczeń przeczytał książkę liczącą 480 stron, przy czym każdego dnia czytał taką samą liczbę stron. Gdyby czytał każdego dnia o 8 stron więcej to przeczytałby tę książkę o 3 dni wcześniej. Ile dni czytał tę książkę?
Dwa pociągi towarowe wyjechały z miast 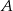 i
i 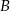 oddalonych od siebie o 540 km. Pociąg jadący z miasta
oddalonych od siebie o 540 km. Pociąg jadący z miasta 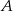 do miasta
do miasta 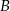 wyjechał o godzinę wcześniej niż pociąg jadący z miasta
wyjechał o godzinę wcześniej niż pociąg jadący z miasta 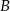 do miasta
do miasta  i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
i jechał z prędkością o 9 km/h mniejszą. Pociągi te minęły się w połowie drogi. Oblicz, z jakimi prędkościami jechały te pociągi.
Cena produktu po podniesieniu stawki VAT z 7% do 22% wzrosła o 90 zł. Ile jest równa nowa cena produktu?
Rafał wpłacił 300 zł do banku. Oprocentowanie w stosunku rocznym wynosi 12% i jest kapitalizowane miesięcznie. Ile pieniędzy wraz z odsetkami będzie miał po 9 miesiącach, zakładając, że oprocentowanie nie ulegnie zmianie?
Taras znajduje się na wysokości 9m i 35cm nad powierzchnią ziemi. Schody prowadzące na taras zostały tak zaprojektowane, że wysokość pierwszego stopnia jest równa 32cm, a każdy następny stopień jest o 0,5 cm niższy od poprzedniego. Ile stopni mają te schody?
Uzasadnij, że nie istnieją dwie liczby, których suma jest równa 4, a iloczyn jest równy 5.
Liczbę 49 rozłóż na dwa dodatnie składniki tak, aby ich iloczyn był największy. Podaj wartość iloczynu.
Oblicz sumę tych liczb naturalnych, które przy dzieleniu przez 4 dają resztę 3 i są mniejsze od 300.
W klasie na początku roku było 30 uczniów. W ciągu roku z klasy odeszło 20% dziewcząt i przybyło 60% chłopców. Na koniec roku liczba dziewcząt i chłopców w klasie była równa. Ile dziewcząt, i ilu chłopców liczyła klasa na początku roku?
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?

