Zestaw użytkownika nr 7030_9515
Zestaw użytkownika
nr 7030_9515
Napisz równanie okręgu, którego środek należy do osi 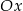 , i który przechodzi przez punkty
, i który przechodzi przez punkty 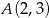 i
i 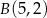 .
.
Dla jakich wartości parametru 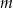 równanie
równanie 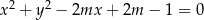 opisuje okrąg?
opisuje okrąg?
- Podaj wspórzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
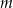 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 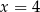 ?
?
Znajdź równanie okręgu stycznego do prostej 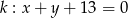 i do prostej
i do prostej 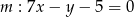 w punkcie
w punkcie 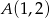 .
.
Środek okręgu przechodzącego przez punkty 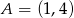 i
i 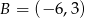 leży na osi
leży na osi 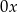 .
.
- Wyznacz równanie tego okręgu.
- Wyznacz równanie prostej prostopadłej do prostej
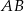 i oddalonej od początku układu współrzędnych o
i oddalonej od początku układu współrzędnych o 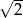 .
.
Określ wzajemne położenie okręgów: 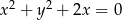 i
i 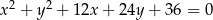 .
.
Wyznacz środek okręgu wpisanego w trójkąt, którego boki zwierają się w prostych o równaniach 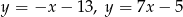 oraz
oraz 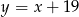 .
.
Znajdź równanie obrazu krzywej 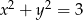 w przesunięciu o wektor
w przesunięciu o wektor ![u = [− 4 ,2 ]](https://img.zadania.info/zad/4910174/HzadT1x.gif) .
.
Napisz równanie okręgu, którego środek znajduje się na prostej 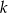 , przechodzącego przez punkty
, przechodzącego przez punkty 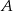 i
i 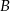 , jeśli
, jeśli 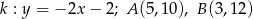 .
.
Przez początek układu współrzędnych poprowadzono prostą przecinającą okrąg 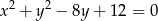 w dwóch punktach
w dwóch punktach 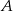 i
i 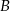 . Uzasadnij, że liczba
. Uzasadnij, że liczba  nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
Napisz równanie okręgu stycznego do osi 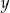 w punkcie
w punkcie 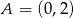 i przechodzącego przez punkt
i przechodzącego przez punkt 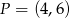 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 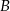 i
i 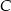 , aby trójkąt
, aby trójkąt 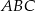 był równoboczny.
był równoboczny.
Znajdź równania prostych stycznych do dwóch okręgów: 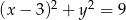 i
i 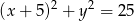 .
.
Dany jest okrąg o równaniu 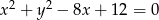 .
.
- Wyznacz równania stycznych do okręgu przechodzących przez początek układu współrzędnych.
- Oblicz pole figury ograniczonej stycznymi i łukiem okręgu wyznaczonym przez punkty styczności.
Dany jest okrąg o równaniu 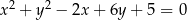 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
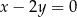 .
. - Oblicz pole trójkąta
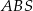 , gdzie
, gdzie 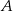 i
i 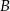 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 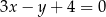 , zaś
, zaś 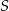 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Dane są figury:
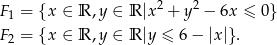
- Narysuj figury
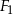 i
i 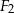 oraz wyznacz figurę
oraz wyznacz figurę 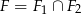 .
. - Oblicz pole figury