Zadanie nr 7132417
Uzasadnij, że suma kątów wewnętrznych dowolnego  –kąta wypukłego jest równa
–kąta wypukłego jest równa 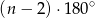 .
.
Rozwiązanie
Sposób I
Podzielmy  –kąt na trójkąty prowadząc wszystkie przekątne z jednego ustalonego wierzchołka.
–kąt na trójkąty prowadząc wszystkie przekątne z jednego ustalonego wierzchołka.
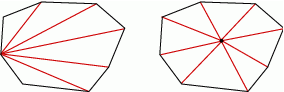
Ponieważ z wierzchołka wychodzi 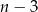 przekątnych, więc otrzymamy
przekątnych, więc otrzymamy 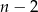 trójkątów. Suma kątów tych trójkątów to dokładnie suma kątów wewnętrznych
trójkątów. Suma kątów tych trójkątów to dokładnie suma kątów wewnętrznych  –kąta, co daje nam żądaną równość.
–kąta, co daje nam żądaną równość.
Sposób II
Możemy wielokąt podzielić na trójkąty jeszcze w inny sposób: wybierzmy dowolny punkt wewnątrz wielokąta i połączmy go odcinkami ze wszystkimi wierzchołkami. W ten sposób dostajemy  trójkątów. Tym razem jednak suma kątów trójkątów jest większa od sumy kątów wielokąta o kąt
trójkątów. Tym razem jednak suma kątów trójkątów jest większa od sumy kątów wielokąta o kąt 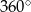 (kąt wokół wybranego punktu). Zatem szukana suma to
(kąt wokół wybranego punktu). Zatem szukana suma to
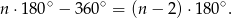
Wprawdzie ten sposób może się wydawać bardziej skomplikowany, ale ma on olbrzymią zaletę w stosunku do poprzedniego, mianowicie można go zastosować w przypadku wielu wielokątów, które nie są wypukłe. Aby przedstawione rozumowanie działało wystarczy, aby w wielokącie istniał punkt, który można połączyć odcinkami ze wszystkimi wierzchołkami (są to tzw. wielokąty gwiaździste).
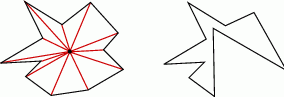
Okazuje się, że ten sam wzór jest też prawdziwy dla dowolnych wielokątów, ale dowód w tym przypadku jest znacznie trudniejszy.

