Zestaw użytkownika nr 7137_3112

Zestaw użytkownika
nr 7137_3112

Zadanie 1
(5 pkt)

Podstawą graniastosłupa prawidłowego jest trójkąt, w którym długość wysokości wynosi 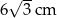√ -- 6 3cm . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt o mierze 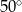50∘ . Oblicz pole powierzchni całkowitej i objętość graniastosłupa. Wynik podaj z dokładnością do 1cm.

Zadanie 2
(5 pkt)

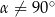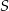W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę r wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna r z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α ⁄= 90∘ . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę r jest równe S . Oblicz objętość graniastosłupa.

Zadanie 3
(5 pkt)

Podstawą graniastosłupa jest trapez równoramienny o podstawach długości 56cm i 40cm oraz wysokości 15cm. Wiedząc, że wysokość graniastosłupa jest równa 10cm, oblicz jego pole powierzchni całkowitej.

Zadanie 4
(5 pkt)

Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.

Zadanie 5
(5 pkt)

W ostrosłupie 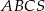ABCS podstawa 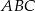ABC jest trójkątem prostokątnym, 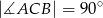|∡ACB | = 90∘ . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10cm. Wysokość 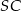SC ostrosłupa ma długość 24cm. Oblicz:

  • objętość ostrosłupa;
  • tangens kąta nachylenia ściany bocznej ostrosłupa, zawierającej przeciwprostokątną podstawy, do płaszczyzny podstawy.
Zadanie 6
(5 pkt)

Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.

Zadanie 7
(5 pkt)

Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz stosunek objętości stożka do objętości wpisanej w niego kuli.

Zadanie 8
(5 pkt)

Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 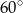60 ∘ . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?

Zadanie 9
(5 pkt)

Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 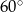60∘ . Oblicz objętość walca.

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze