Zestaw użytkownika nr 7212_7479

Zestaw użytkownika
nr 7212_7479

Zadanie 1

Prostokąt 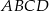ABCD obracając się wokół boku 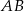, zakreślił walec 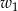w 1 . Ten sam prostokąt obracając się wokół boku 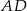, zakreślił walec 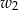. Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt 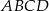ABCD jest kwadratem.

Zadanie 2

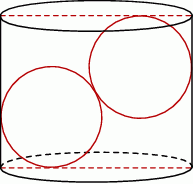
W pojemniku o kształcie walca o promieniu podstawy 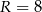R = 8 umieszczono dwie kule o promieniu 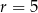r = 5 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.

Zadanie 3

Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 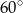60 ∘ . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?

Zadanie 4

Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości 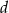tworzy z wysokością kąt o mierze .

Wyprowadź wzór na objętość walca.
Oblicz tę objętość dla 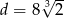i .

Zadanie 5

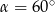Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 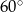60∘ . Oblicz objętość walca.

Zadanie 6

Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?

Zadanie 7

Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest prostokątem. Przekątna tego prostokąta ma długość 12 i tworzy z bokiem, którego długość jest równa wysokości walca, kąt o mierze 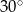30∘ .

Oblicz pole powierzchni bocznej tego walca.
Sprawdź, czy objętość tego walca jest większa od 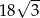. Odpowiedź uzasadnij.

Zadanie 8

Promień i wysokość walca mają jednakową długość. Pole powierzchni bocznej wynosi 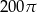200 π . Oblicz pole podstawy walca.

Arkusz Wersja PDF