/Szkoła średnia/Zadania maturalne/Matura 2014/Matura próbna/Zadania.info

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 3 maja 2014 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Rozwiąż nierówność 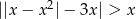2 ||x− x |− 3x | > x .

Zadanie 2
(3 pkt)

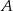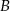Do dwóch okręgów przecinających się w punktach A i B poprowadzono wspólną styczną 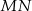MN , przy czym punkt 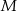M należy do pierwszego, a punkt 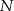N do drugiego okręgu. Wykaż, że prosta 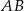AB dzieli odcinek 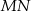MN na połowy.

Zadanie 3
(4 pkt)

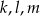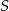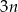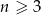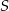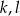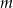Proste k,l,m są parami różne i równoległe. Na prostych tych wybrano zbiór S składający się z 3n punktów (n ≥ 3 ), przy czym na każdej z prostych wybrano n punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru S leżą na jednej prostej, to prostą tą jest k ,l lub m . Oblicz ile jest trójkątów o wierzchołkach należących do zbioru S .

Zadanie 4
(5 pkt)

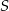Rozwiąż nierówność 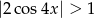|2c os4x | > 1 .

Zadanie 5
(5 pkt)

Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.

Zadanie 6
(5 pkt)

Wyznacz wszystkie wartości parametru 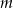m , dla których jeden z pierwiastków równania

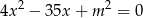
2 2 4x − 35x + m = 0

jest kwadratem drugiego pierwiastka. Oblicz te pierwiastki.

Zadanie 7
(5 pkt)

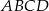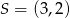W czworokącie ABCD dane są −→ − → AB = [6,− 3],DA = [− 8,− 7] oraz środek S = (3,2) przekątnej 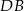DB . Wyznacz współrzędne rzutu prostopadłego punktu 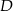D na prostą AB .

Zadanie 8
(5 pkt)

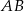Wyznacz wszystkie wartości parametrów 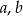a,b , dla których nierówność

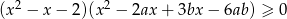
2 2 (x − x − 2)(x − 2ax + 3bx − 6ab) ≥ 0

jest spełniona przez każdą liczbę rzeczywistą.

Zadanie 9
(6 pkt)

Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 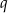q , a cosinus jednego z jego kątów jest równy q − 4 .

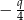  • Wyznacz q .
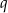  • Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość 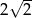√ -- 2 2 , oblicz pole tego trójkąta.

Zadanie 10
(4 pkt)

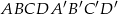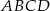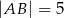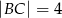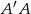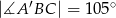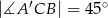Podstawą graniastosłupa prostego ABCDA ′B′C ′D ′ jest równoległobok ABCD o bokach długości |AB | = 5 i |BC | = 4 . Oblicz długość wysokości ′ A A graniastosłupa jeżeli ′ ∘ |∡A BC | = 105 oraz ′ ∘ |∡A CB | = 45 .

Zadanie 11
(3 pkt)

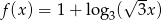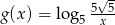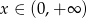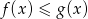Naszkicuj wykresy funkcji √ -- f(x) = 1+ log 3( 3x) i 5√ 5 g(x) = lo g5--x- , gdzie x ∈ (0,+ ∞ ) . Odczytaj z wykresów zbiór rozwiązań nierówności f(x) ≤ g(x) .

Arkusz Wersja PDF
Rozwiązania