Zestaw użytkownika nr 7296_2275

Zestaw użytkownika
nr 7296_2275

Zadanie 1

(5 pkt)

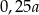Czworościan foremny o krawędzi rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości 0,25a od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.

Zadanie 2

(5 pkt)

Oblicz objętość czworościanu foremnego o krawędzi .

Zadanie 3

(5 pkt)

Oblicz stosunek objętości kuli wpisanej w czworościan foremny do objętości kuli opisanej na tym czworościanie.

Zadanie 4

(5 pkt)

Wysokość czworościanu foremnego ma długość 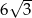√ -- 6 3 . Oblicz jego objętość i pole powierzchni całkowitej.

Zadanie 5

(5 pkt)

Objętość graniastosłupa prawidłowego trójkątnego jest równa 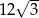√ -- 12 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.

Zadanie 6

(5 pkt)

W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.

Zadanie 7

(5 pkt)

Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 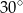30 ∘ .

Zadanie 8

(5 pkt)

Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 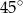45 ∘ obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.

Zadanie 9

(5 pkt)

Trapez prostokątny obraca się wokół boku tworzącego z podstawami kąty proste. Podstawy trapezu mają długość odpowiednio 10 i 7. Pole trapezu wynosi 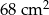68cm 2 . Oblicz objętość otrzymanej bryły.

Zadanie 10

(5 pkt)

Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.

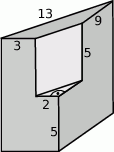
Oblicz objętość tej konstrukcji.
Oblicz łączne pole powierzchni wszystkich 7 ścian otrzymanej bryły. Wynik podaj z zaokrągleniem do .

Zadanie 11

(5 pkt)

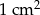Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 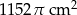2 1152π cm .

Zadanie 12

(5 pkt)

Ołowianą kulę o średnicy 60 cm przetopiono na walce o wysokości i promieniu podstawy równych 2 cm. Ile takich walców otrzymano?

Zadanie 13

(5 pkt)

W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 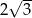√ -- 2 3 . Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem 45 ∘ .

Zadanie 14

(5 pkt)

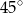W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 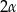. Oblicz objętość tego ostrosłupa.

Zadanie 15

(5 pkt)

Podstawą ostrosłupa jest romb o boku długości 18cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 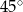45∘ . Pole powierzchni bocznej ostrosłupa jest równe 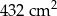432cm 2 . Oblicz jego objętość.

Zadanie 16

(5 pkt)

Przekątna prostopadłościanu ma długość 8 cm, a miara kąta, jaki tworzy ona ze ścianą boczną wynosi 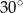30∘ . Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi √ -- 2 7 cm .

Zadanie 17

(5 pkt)

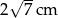W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 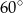60∘ , oblicz pole powierzchni tego prostopadłościanu.

Zadanie 18

(5 pkt)

Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz miarę kąta rozwarcia tego stożka.

Zadanie 19

(5 pkt)

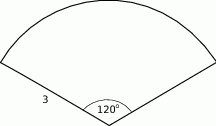
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 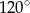120∘ (zobacz rysunek). Oblicz objętość tego stożka.

Zadanie 20

(5 pkt)

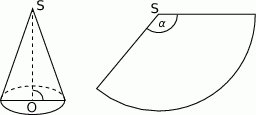
Tworząca stożka ma długość 3 dm. Długość promienia podstawy stożka jest równa 1 dm. Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła. Oblicz miarę kąta środkowego tego wycinka.

Zadanie 21

(5 pkt)

Stożek, którego pole powierzchni bocznej jest równe 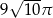√ --- 9 10π , jest wpisany w kulę o promieniu 5. Oblicz objętość stożka.

Zadanie 22

(5 pkt)

Przekątna sześcianu jest o 3 dłuższa od krawędzi sześcianu. Oblicz objętość tego sześcianu.

Zadanie 23

(5 pkt)

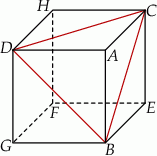
W narysowanym obok sześcianie krawędź ma długość . Oblicz odległość wierzchołka 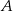od płaszczyzny przechodzącej przez wierzchołki 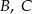B, C i .

Zadanie 24

(5 pkt)

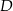Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 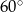60∘ . Oblicz objętość walca.

Zadanie 25

(5 pkt)

W stożek o promieniu podstawy długości 9 i wysokości 12 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 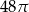48π .

Zadanie 26

(5 pkt)

Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 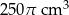250πcm 3 zużyć jak najmniej materiału na jej wykonanie.

Arkusz Wersja PDF