Zestaw użytkownika nr 7417_9704
Stereometria-sprawdzianCzas pracy: 45 min.Suma punktów: 18
Graniastosłup, który ma 22 ściany, ma
A) 40 wierzchołków B) 20 wierzchołków C) 42 wierzchołki D) 22 wierzchołki
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu 12 cm. Podstawa tego stożka jest kołem o promieniu
A) 6 cm B) 12 cm C) 1 cm D) 3 cm
Kula ma objętość 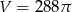 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 9 B) 12 C) 6 D) 8
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 90. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 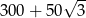 B)
B) 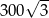 C) 300 D)
C) 300 D) 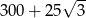
Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 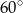 . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
. Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?
Oblicz objętość i pole powierzchni graniastosłupa, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 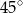 .
.
Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 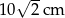 . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze
. Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 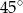 . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Dany jest graniastosłup prawidłowy trójkątny 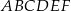 o podstawach
o podstawach 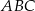 i
i 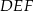 i krawędziach bocznych
i krawędziach bocznych 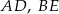 i
i 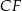 . Oblicz pole trójkąta
. Oblicz pole trójkąta 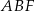 wiedząc, że
wiedząc, że 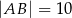 i
i 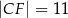 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 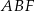 .
.

