Zestaw użytkownika nr 7427_6250

Zestaw użytkownika
nr 7427_6250

Zadanie 1
(2 pkt)

Podaj miejsca zerowe funkcji 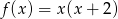f(x ) = x(x + 2) .

Zadanie 2
(3 pkt)

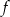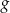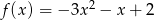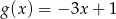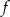Funkcje f i g dane są wzorami 2 f(x) = − 3x − x+ 2 , g(x) = − 3x+ 1 . Wyznacz zbiór argumentów x , dla których funkcja f przyjmuje wartości większe od funkcji g .

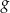Zadanie 3
(2 pkt)

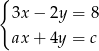
Dla jakich współczynników a i c układ { 3x − 2y = 8 ax + 4y = c

  • ma nieskończenie wiele rozwiązań;
  • jest sprzeczny?
Zadanie 4
(4 pkt)

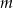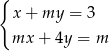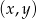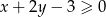Dla jakich wartości parametru m rozwiązaniem układu { x + my = 3 mx + 4y = m jest para liczb (x,y) spełniająca nierówność x + 2y − 3 ≥ 0 ?

Zadanie 5
(5 pkt)

Pierwiastkami wielomianu 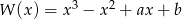3 2 W (x ) = x − x + ax + b są tylko dwie liczby: 2 oraz (-3).

  • Oblicz a i b .
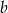  • Zapisz wielomian w postaci czynników liniowych.
Zadanie 6
(5 pkt)

Dany jest wielomian 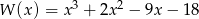3 2 W (x) = x + 2x − 9x − 18 .

  • Wyznacz pierwiastki tego wielomianu.
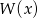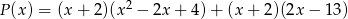  • Sprawdź, czy wielomiany W (x ) i P(x ) = (x+ 2)(x2 − 2x + 4) + (x + 2)(2x − 1 3) są równe.
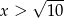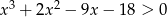  • Uzasadnij, że jeśli √ --- x > 10 , to 3 2 x + 2x − 9x − 18 > 0 .
Zadanie 7
(4 pkt)

Wyznacz zbiory:

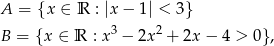
A = {x ∈ R : |x − 1| < 3} B = {x ∈ R : x3 − 2x2 + 2x − 4 > 0},

a następnie wyznacz zbiór 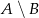A ∖ B .

Zadanie 8
(3 pkt)

Wyznacz największą liczbę całkowitą spełniającą nierówność

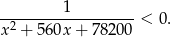
1 --2----------------< 0. x + 5 60x + 78200
Zadanie 9
(3 pkt)

Rozwiąż równanie 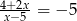4+2x- x− 5 = − 5 .

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze