Zestaw użytkownika nr 7470_1302
Zestaw użytkownika
nr 7470_1302
Liczba 2 jest miejscem zerowym wielomianu 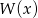 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 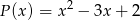 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 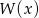 przez dwumian
przez dwumian 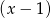 otrzymujemy resztę 5.
otrzymujemy resztę 5.
Reszta z dzielenia wielomianu 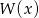 przez dwumian
przez dwumian 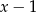 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 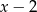 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 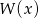 przez wielomian
przez wielomian 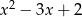 .
.
Przedstaw wielomian 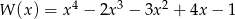 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
Dana jest funkcja 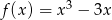 dla
dla 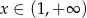 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 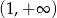 .
.
Wielomian 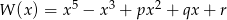 jest podzielny przez wielomian
jest podzielny przez wielomian 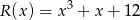 . Wyznacz liczby
. Wyznacz liczby 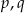 i
i  .
.
Wielomian 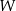 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 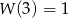 oraz
oraz 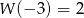 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 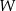 są liczbami całkowitymi.
są liczbami całkowitymi.
Wyznacz zbiór wartości funkcji 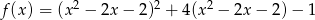 .
.
Oblicz najmniejszą wartość wielomianu 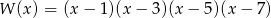 .
.
Rozłóż na czynniki drugiego stopnia wielomian 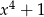 .
.
Wielomian 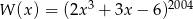 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 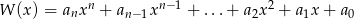 . Oblicz sumę
. Oblicz sumę 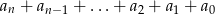 .
.
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 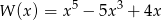 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
Wykaż, że wielomian 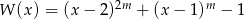 jest podzielny przez wielomian
jest podzielny przez wielomian 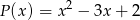 dla każdego
dla każdego 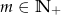 .
.
Liczba -7 jest miejscem zerowym 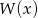 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 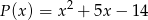 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 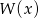 przez dwumian
przez dwumian 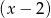 otrzymujemy resztę 18.
otrzymujemy resztę 18.

