Zestaw użytkownika nr 7529_1684
Geometria analitycznaCzas pracy: 45 min.Suma punktów: 20
Proste o równaniach 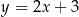 oraz
oraz 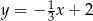
A) przecinają się pod kątem innym niż prosty
B) są prostopadłe
C) pokrywają się
D) są równoległe i różne
Punkty 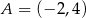 i
i 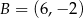 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 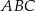 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 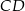 tego trójkąta przecina prostą
tego trójkąta przecina prostą 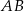 w punkcie
w punkcie
A) 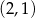 B)
B) 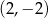 C)
C) 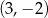 D)
D) 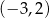
Prostą równoległą do prostej 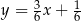 jest prosta:
jest prosta:
A) 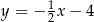 B)
B) 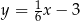 C)
C) 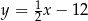 D)
D) 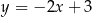
Prosta o równaniu 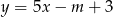 przechodzi przez punkt
przechodzi przez punkt 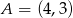 . Wtedy
. Wtedy
A) 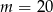 B)
B) 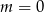 C)
C) 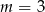 D)
D) 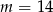
Punkty 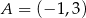 i
i 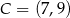 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 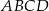 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 5 B) 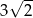 C) 10 D)
C) 10 D) 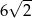
Dane są punkty 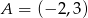 oraz
oraz 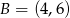 . Długość odcinka
. Długość odcinka 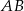 jest równa
jest równa
A) 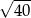 B)
B) 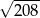 C)
C) 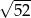 D)
D) 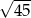
Które z równań opisuje prostą prostopadłą do prostej o równaniu 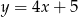 ?
?
A) 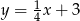 B)
B) 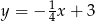 C)
C) 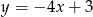 D)
D) 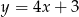
Punkt 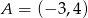 jest początkiem odcinka
jest początkiem odcinka 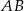 , gdzie
, gdzie 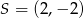 jest jego środkiem. Punkt
jest jego środkiem. Punkt 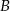 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 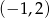 B)
B) 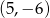 C)
C) 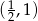 D)
D) 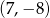
Liczba punktów wspólnych okręgu o równaniu 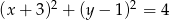 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 1 B) 2 C) 0 D) 4
Proste o równaniach 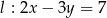 i
i 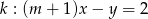 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 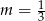 B)
B) 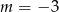 C)
C) 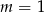 D)
D) 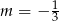
Punkty 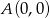 oraz
oraz 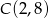 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 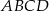 o boku długości
o boku długości 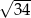 . Wyznacz współrzędne pozostałych wierzchołków tego rombu.
. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Zapisz równanie prostej przechodzącej przez punkt 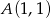 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 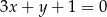 .
.
Oblicz pole trójkąta ograniczonego prostą 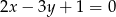 i osiami układu współrzędnych.
i osiami układu współrzędnych.

