Zestaw użytkownika nr 7543_5504
Zestaw użytkownika
nr 7543_5504
Dane są zbiory 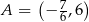 i
i 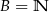 liczb naturalnych dodatnich. Wówczas iloczyn zbiorów
liczb naturalnych dodatnich. Wówczas iloczyn zbiorów 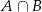 jest równy
jest równy
A) 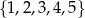 B)
B) 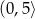 C)
C) 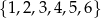 D)
D) 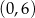
Jeśli 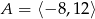 i
i 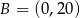 , to różnica
, to różnica 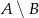 jest przedziałem
jest przedziałem
A) 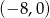 B)
B) 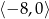 C)
C) 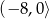 D)
D) 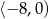
Jeśli 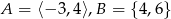 , to różnica
, to różnica 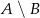 jest równa
jest równa
A) 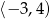 B)
B) 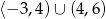 C)
C) 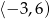 D)
D) 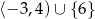
Liczbę 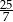 zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
A) 0,8% B) 0,008% C) 8% D) 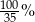
Przybliżenie z nadmiarem liczby dodatniej  wynosi 13. Błąd względny tego przybliżenia wynosi
wynosi 13. Błąd względny tego przybliżenia wynosi 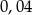 . Wobec tego
. Wobec tego
A) 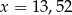 B)
B) 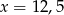 C)
C) 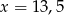 D)
D) 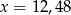
Pierwiastek równania 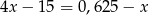 zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
A) 5% B) 7,5% C) 2,4% D) 2,5%
Liczbę 6,49 zaokrąglamy do najbliższej liczby całkowitej. Błąd względny tego przybliżenia z dokładnością do 0,1% jest równy
A) 4,7% B) 7,5% C) 8% D) 7,6%
Po rozłożeniu na czynniki wyrażenie 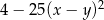 ma postać
ma postać
A) 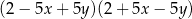
B) 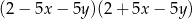
C) 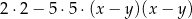
D) 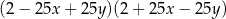
Jeśli 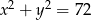 i
i 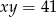 , to kwadrat sumy liczb
, to kwadrat sumy liczb 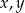 jest równy
jest równy
A) 6865 B) 113 C) 5184 D) 154
Jeżeli 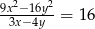 , to
, to
A) 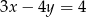 B)
B) 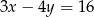 C)
C) 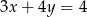 D)
D) 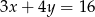
Wyrażenie 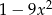 po rozłożeniu na czynniki liniowe ma postać:
po rozłożeniu na czynniki liniowe ma postać:
A) 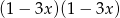 B)
B) 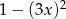 C)
C) 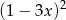 D)
D) 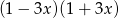
Wyrażenie 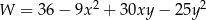 w postaci iloczynowej ma postać
w postaci iloczynowej ma postać
A) 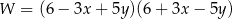
B) 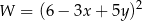
C) 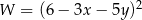
D) 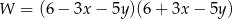
Wyrażenie 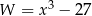 jest równe
jest równe
A) 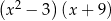
B) 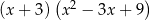
C) 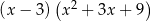
D) 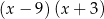
Wyrażenie 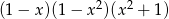 jest równe
jest równe
A) 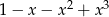 B)
B) 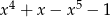 C)
C) 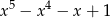 D)
D) 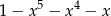
Rozwiązaniem równania 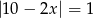 są liczby
są liczby
A) różniące się o 1 B) niewymierne C) całkowite D) przeciwne
Wskaż nierówność, którą spełnia liczba 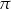 .
.
A) 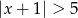 B)
B) 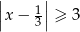 C)
C) 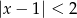 D)
D) 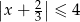
Wyrażenie 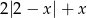 dla
dla 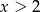 ma wartość
ma wartość
A) 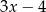 B) 5 C)
B) 5 C) 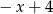 D) 1
D) 1
Odległość liczby  od liczby -8 na osi liczbowej jest równa
od liczby -8 na osi liczbowej jest równa
A) 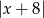 B)
B) 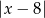 C)
C) 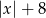 D)
D) 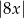
Liczby pierwsze należące jednocześnie do zbioru rozwiązań nierówności 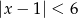 i do zbioru rozwiązań nierówności
i do zbioru rozwiązań nierówności 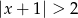 to
to
A) 3,5 B) 1,2,3,5 C) 2,3,5 D) 3,4,5
Liczby całkowite ujemne spełniające nierówność 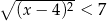 to
to
A) 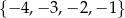
B) 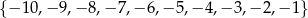
C) 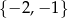
D) 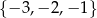
Zbiór liczb, które na osi liczbowej są równoodległe od liczb 4 i -10, można opisać za pomocą równania
A) 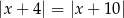
B) 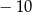
C) 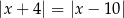
D) 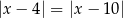
Liczba 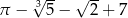 jest rozwiązaniem równania
jest rozwiązaniem równania 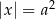 z niewiadomą
z niewiadomą  . Która z podanych liczb jest również rozwiązaniem tego równania?
. Która z podanych liczb jest również rozwiązaniem tego równania?
A) 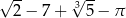
B) 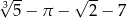
C) 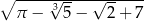
D) 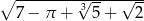
Liczba 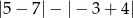 jest równa
jest równa
A) -5 B) -3 C) 3 D) 1
Rozwiązaniem nierówności 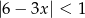 jest zbiór
jest zbiór
A) 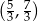 B)
B) 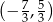 C)
C) 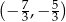 D)
D) 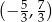
Rozwiązaniem równania 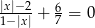 są liczby
są liczby
A) 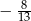 i
i 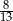 B)
B) 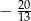 i
i 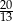 C) -8 i 8 D) -20 i 20
C) -8 i 8 D) -20 i 20
Przedział 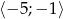 zapisany za pomocą wartości bezwzględnej to:
zapisany za pomocą wartości bezwzględnej to:
A) 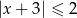 B)
B) 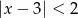 C)
C) 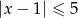 D)
D) 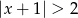
Wartość wyrażenia 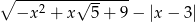 dla
dla 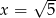 jest równa
jest równa
A) 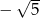 B)
B) 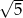 C)
C) 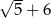 D)
D) 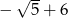
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 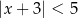 B)
B) 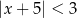 C)
C) 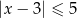 D)
D) 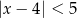
Wskaż rysunek, który może przedstawiać zbiór rozwiązań nierówności 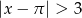 .
.
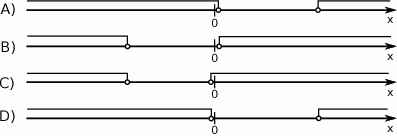
Ile liczb naturalnych należy do zbioru rozwiązań nierówności 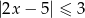 ?
?
A) 4 B) 3 C) 2 D) 0
Jeśli 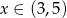 , to wyrażenie
, to wyrażenie 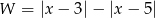 można przedstawić w postaci
można przedstawić w postaci
A) 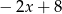 B) 2 C)
B) 2 C) 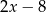 D) -2
D) -2
Równanie 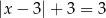 ma:
ma:
A) dwa rozwiązania
B) jedno rozwiązanie
C) zero rozwiązań
D) nieskończenie wiele rozwiązań
Rozwiązaniem nierówności 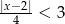 jest zbiór
jest zbiór
A) 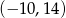 B)
B) 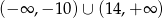 C)
C) 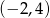 D)
D) 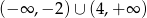
Przedział 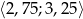 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 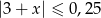 B)
B) 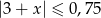 C)
C) 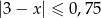 D)
D) 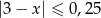
Zbiór zaznaczony na rysunku poniżej
![]()
jest zbiorem rozwiązań nierówności
A) 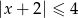 B)
B) 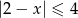 C)
C) 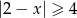 D)
D) 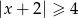
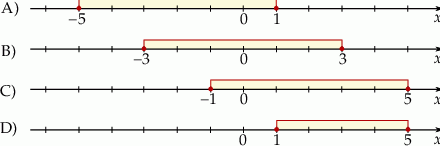
Który z zaznaczonych przedziałów jest zbiorem rozwiązań nierówności 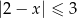 .
.
Niech 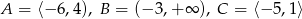 . Wyznacz zbiór
. Wyznacz zbiór 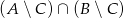 .
.
- Zaznacz na osi liczbowej i zapisz w postaci przedziału zbiór wszystkich liczb rzeczywistych, których odległość na osi liczbowej od liczby (-1) jest nie większa niż 4.
- Liczba 6,5 stanowi 175% liczby
 . Sprawdź czy liczba
. Sprawdź czy liczba  należy do danego przedziału.
należy do danego przedziału.
Wyznacz algebraicznie zbiór tych wszystkich punktów 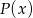 osi liczbowej, których suma odległości od punktów
osi liczbowej, których suma odległości od punktów 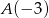 oraz
oraz 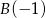 jest mniejsza od 5.
jest mniejsza od 5.
Na osi liczbowej zaznaczono przedział 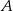 złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział
złożony z tych liczb rzeczywistych, których odległość od punktu 1 jest niewiększa od 4,5. Przedział 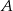 przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział
przesunięto wzdłuż osi o 2 jednostki w kierunku dodatnim, otrzymując przedział 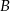 . Wyznacz wszystkie liczby całkowite, które należą jednocześnie do
. Wyznacz wszystkie liczby całkowite, które należą jednocześnie do 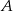 i do
i do 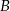 .
.

