Zestaw użytkownika nr 7555_9824
Stereometria - sprawdzianCzas pracy: 45 min.
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 25 C) 22 D) 26
Kąt rozwarcia stożka ma miarę 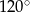 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 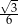 B)
B) 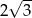 C)
C) 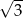 D)
D) 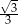
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
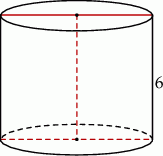
A) 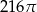 B)
B) 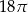 C)
C) 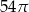 D)
D) 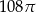
Promień podstawy walca zwiększamy cztery razy, a jego wysokość zmniejszamy cztery razy. Wówczas objętość walca
A) nie zmieni się
B) zwiększy się o cztery
C) zmniejszy się cztery razy
D) zwiększy się cztery razy
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 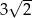 . Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze
. Przekątna tego graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze 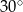 . Wysokość tego graniastosłupa ma długość
. Wysokość tego graniastosłupa ma długość
A) 4 B) 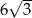 C) 6 D)
C) 6 D) 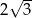
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 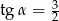 B)
B) 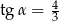 C)
C) 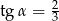 D)
D) 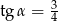
Długość, szerokość i wysokość prostopadłościanu są w stosunku 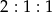 . Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
. Przekątna prostopadłościanu ma długość 6. Pole podstawy prostopadłościanu jest równe
A) 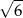 B) 24 C) 12 D) 6
B) 24 C) 12 D) 6
Powierzchnia sześcianu wynosi 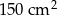 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 5 cm B) 4 cm C) 5,5 cm D) 6 cm
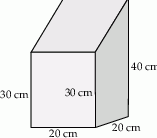
Narysowana bryła ma w podstawie kwadrat, a krawędzie boczne są prostopadłe do podstawy. Objętość tej bryły jest równa
A) 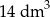 B)
B) 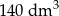 C)
C) 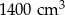 D)
D) 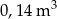
Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 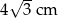 .
.
Objętość stożka, w którym wysokość jest równa promieniowi podstawy, jest równa 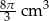 . Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie
. Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie 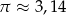 podaj wynik z dokładnością do 0,1.
podaj wynik z dokładnością do 0,1.
Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 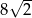 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 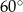 . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
. Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.

