/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 29 lutego 2020 Czas pracy: 180 minut
Zadania zamknięte
Parametr 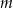 dobrano tak, że rozwiązaniem nierówności
dobrano tak, że rozwiązaniem nierówności
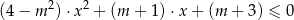
z niewiadomą  jest przedział postaci
jest przedział postaci 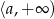 . Wynika stąd, że
. Wynika stąd, że
A) 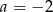 B)
B) 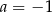 C)
C) 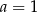 D)
D) 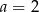
Liczba 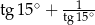 jest równa
jest równa
A) 4 B) 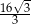 C) 1 D)
C) 1 D) 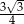
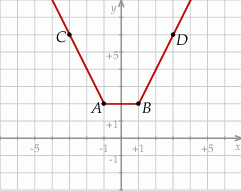
Na rysunku przedstawiono fragment wykresu funkcji 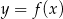 , który jest złożony z dwóch półprostych
, który jest złożony z dwóch półprostych 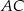 i
i 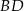 oraz odcinka
oraz odcinka 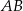 , gdzie
, gdzie 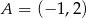 ,
, 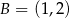 ,
, 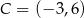 ,
, 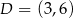 .
.
Wzór funkcji 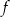 to
to
A) 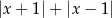 B)
B) 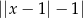 C)
C) 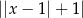 D)
D) 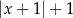
Dziedziną funkcji określonej wzorem 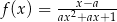 jest zbiór liczb rzeczywistych. To oznacza, że liczba
jest zbiór liczb rzeczywistych. To oznacza, że liczba  nie może być równa
nie może być równa
A) 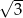 B) 0 C)
B) 0 C) 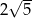 D)
D) 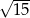
Na bokach 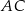 i
i 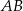 trójkąta
trójkąta 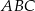 o wierzchołkach
o wierzchołkach 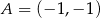 ,
, 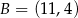 i
i 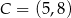 , wybrano punkty
, wybrano punkty 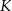 i
i 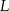 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 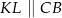 . Pole trapezu
. Pole trapezu 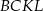 stanowi
stanowi 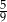 pola trójkąta
pola trójkąta 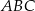 . Zatem
. Zatem
A) 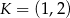 B)
B) 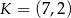 C)
C) 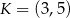 D)
D) 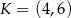
Zadania otwarte
W urnie znajduje się 18 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 6 kul białych i 12 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul czarnych.
Oblicz granicę 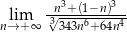 .
.
W czworokącie wypukłym 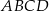 , długości boków
, długości boków 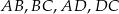 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
Oblicz odległość między stycznymi do wykresu funkcji 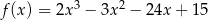 , które są równoległe do prostej
, które są równoległe do prostej 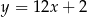 .
.
Udowodnij, że jeżeli liczba całkowita  nie jest podzielna przez 3, to wyrażenie
nie jest podzielna przez 3, to wyrażenie 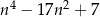 jest podzielne przez 9.
jest podzielne przez 9.
Niech 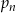 , dla liczby całkowitej
, dla liczby całkowitej 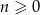 , oznacza sumę odwrotności pierwiastków równania
, oznacza sumę odwrotności pierwiastków równania
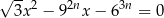
z niewiadomą  . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 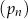 .
.
Liczba przekątnych  –kąta foremnego jest o 73 mniejsza niż liczba przekątnych
–kąta foremnego jest o 73 mniejsza niż liczba przekątnych 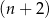 –kąta. Oblicz
–kąta. Oblicz  .
.
Rozwiąż równanie 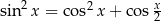 w przedziale
w przedziale 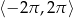 .
.
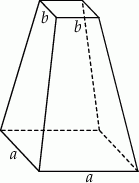
Przedstawiona na rysunku bryła to ostrosłup prawidłowy czworokątny ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 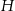 , a
, a  i
i 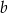 (
(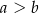 ) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
Dane są okręgi o równaniach 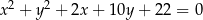 i
i 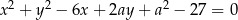 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy 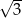 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
Rozważamy wszystkie walce o objętości 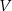 . Wyznacz wysokość i promień podstawy tego z rozważanych walców, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to pole.
. Wyznacz wysokość i promień podstawy tego z rozważanych walców, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to pole.

