Zestaw użytkownika nr 7610_7167
Zestaw użytkownika
nr 7610_7167
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Określ liczbę pierwiastków równania 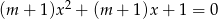 w zależności od wartości parametru
w zależności od wartości parametru 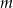 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

Dla jakich wartości parametru  odległość punktu
odległość punktu 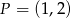 od prostej
od prostej 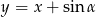 jest mniejsza lub równa
jest mniejsza lub równa 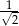 .
.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia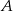 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,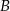 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 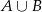 .
.
Wykaż, że jeżeli 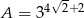 i
i 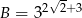 , to
, to 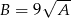 .
.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 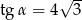 oblicz wartość wyrażenia
oblicz wartość wyrażenia 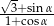 .
.
Dany jest ciąg arytmetyczny 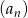 dla
dla 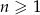 , w którym
, w którym 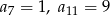 .
.
- Oblicz pierwszy wyraz
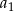 i różnicę
i różnicę  ciągu
ciągu 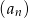 .
. - Sprawdź, czy ciąg
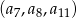 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 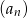 miała wartość najmniejszą.
miała wartość najmniejszą.
W trójkącie 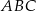 długości boków
długości boków 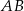 i
i 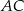 są odpowiednio równe 4 i 6, a długość środkowej
są odpowiednio równe 4 i 6, a długość środkowej 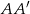 jest równa
jest równa 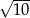 . Oblicz długość boku
. Oblicz długość boku 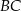 .
.
Suma dwóch liczb jest równa 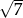 , a ich różnica
, a ich różnica 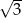 . Oblicz iloczyn tych liczb.
. Oblicz iloczyn tych liczb.
Taryfa dzienna zużycia energii na godzinę wynosi 20 gr, a nocna 12 gr. Ile godzin trwa taryfa nocna, a ile dzienna, jeśli wiadomo, że średnia to 18gr?

