Zestaw użytkownika nr 7647_6278
Zestaw użytkownika
nr 7647_6278
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 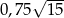 .
.
Pierwszy, trzeci i jedenasty wyraz ciągu arytmetycznego o różnicy 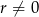 są kolejnymi wyrazami ciągu geometrycznego o ilorazie
są kolejnymi wyrazami ciągu geometrycznego o ilorazie 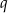 . Dla jakich wartości parametru
. Dla jakich wartości parametru 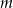 funkcja
funkcja 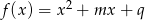 osiąga minimum większe od -196?
osiąga minimum większe od -196?
Wyznacz liczbę  tak, aby liczby dodatnie
tak, aby liczby dodatnie 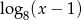 ,
, 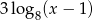 , 6 tworzyły ciąg geometryczny (w podanej kolejności).
, 6 tworzyły ciąg geometryczny (w podanej kolejności).
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 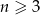 wyraża się wzorem
wyraża się wzorem 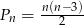 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
W trójkąt równoboczny o boku długości  wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
Wyznacz wszystkie ciągi geometryczne o wyrazach różnych od zera, w których każdy wyraz, rozpoczynając od wyrazu trzeciego, jest równy średniej arytmetycznej dwóch poprzednich wyrazów.
Jednym z pierwiastków trójmianu kwadratowego 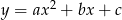 jest -0,2. Liczby
jest -0,2. Liczby 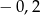 tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
Jedno z rozwiązań równania 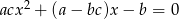 z niewiadomą
z niewiadomą  jest równe 4. Liczby
jest równe 4. Liczby 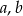 i
i  (w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
(w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 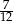 .
.
W ciągu arytmetycznym 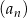 dane są wyrazy:
dane są wyrazy: 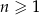 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 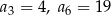 , dla których wyrazy ciągu
, dla których wyrazy ciągu  są mniejsze od 200.
są mniejsze od 200.
Wykaż, że jeżeli liczby 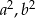 i
i 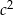 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 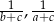 i
i 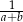 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Liczby 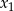 i
i 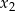 są różnymi miejscami zerowymi funkcji kwadratowej
są różnymi miejscami zerowymi funkcji kwadratowej 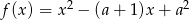 . Dla jakich
. Dla jakich 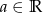 ciąg
ciąg 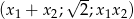 jest geometryczny?
jest geometryczny?
Różnica między drugim wyrazem ciągu geometrycznego a pierwszym wyrazem tego ciągu wynosi -6, a różnica między czwartym a pierwszym wyrazem tego ciągu jest równa -18. Oblicz trzeci wyraz tego ciągu.
Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi oraz siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.
Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.
Cztery liczby tworzą ciąg geometryczny. Jeżeli od pierwszej z nich odejmiemy 2, od drugiej 3, od trzeciej 9, a od czwartej 25, to otrzymane różnice utworzą ciąg arytmetyczny. Znajdź te liczby.
Dla jakich wartości  liczby
liczby 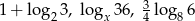 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 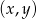 , dla których ciąg:
, dla których ciąg: 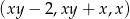 jest rosnącym ciągiem arytmetycznym.
jest rosnącym ciągiem arytmetycznym.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Trzy liczby tworzą ciąg geometryczny. Jeżeli drugą z nich zwiększymy o 8, to otrzymamy ciąg arytmetyczny. Jeżeli trzeci wyraz otrzymanego ciągu arytmetycznego zwiększymy o 64 to znów otrzymamy ciąg geometryczny. Wyznacz te liczby.
Pierwszy wyraz niemonotonicznego ciągu geometrycznego 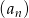 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
- Oblicz iloraz ciągu
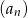 .
. - Oblicz ósmy wyraz ciągu
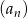 .
. - Suma kilku początkowych wyrazów ciągu
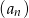 jest równa
jest równa 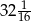 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.
Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli obwód prostokąta jest równy 14.
Wykaż, że jeżeli ciąg 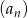 jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym
jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym 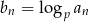 , dla
, dla 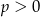 i
i 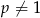 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Dane są dwa ciągi rosnące: arytmetyczny 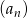 i geometryczny
i geometryczny 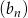 . Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
. Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
Ciąg 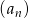 określony jest rekurencyjnie:
określony jest rekurencyjnie: 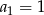 ,
, 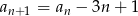 dla
dla 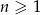 .
.
- Oblicz 4 wyraz ciągu
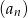 .
. - Zbadaj monotoniczność ciągu
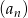 .
.
Wymiary prostopadłościanu o objętości 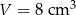 i polu powierzchni całkowitej
i polu powierzchni całkowitej 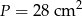 tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
tworzą ciąg geometryczny. Wyznacz długości krawędzi bryły.
Ile liczb trzeba wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny, którego suma jest równa 2008? Wyznacz różnicę tego ciągu.
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Jedna z przyprostokątnych ma długość 6. Jaką długość ma druga przyprostokątna oraz przeciwprostokątna?
Wyznacz wszystkie wartości 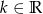 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 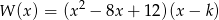 są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.
W skończonym ciągu geometrycznym 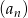 wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.
wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.
Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 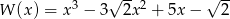 , a jednym z nich jest
, a jednym z nich jest 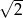 .
.
- Znajdź pierwszy wyraz tego ciągu.
- Oblicz sumę
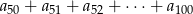 .
.
Wyznacz  tak, aby ciąg
tak, aby ciąg 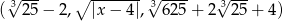 był ciągiem geometrycznym.
był ciągiem geometrycznym.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 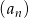 , w którym
, w którym 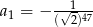 oraz
oraz 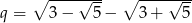 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Ciąg geometryczny 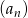 jest określony wzorem
jest określony wzorem 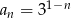 dla
dla 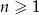 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
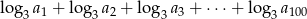 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
Znajdź wartość parametru 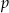 , dla której granica ciągu
, dla której granica ciągu 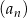 określonego wzorem
określonego wzorem
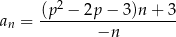
jest równa 4. Zbadaj monotoniczność ciągu 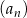 dla zanalezionej wartości
dla zanalezionej wartości 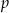 .
.

