Zestaw użytkownika nr 7675_5546
zadania optymalizacyjne
Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.
W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór 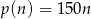 , gdzie
, gdzie  oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność
oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność 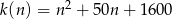 .
.
- Napisz wzór funkcji
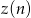 - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
- zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji. - Przy jakiej wielkości produkcji zysk wynosi 0?
- Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?
W skarbcu królewskim było 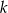 monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę
monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę 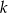 , dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości
, dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości 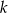 oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
Właściciel sklepu muzycznego „Tra-la-la” kupuje w hurtowni płyty zespołu „Emotion” po 30 zł za sztukę i sprzedaje 56 sztuk miesięcznie, po 50 zł za sztukę. Badania rynku wykazały, że każda obniżka ceny płyty o 1 zł, zwiększy liczbę sprzedanych płyt o 4 sztuki (miesięcznie).
- Wyznacz wzór funkcji miesięcznego zysku właściciela sklepu „Tra-la-la” w zależności od obniżki ceny płyty zespołu „Emotion” (w pełnych złotych). Podaj dziedzinę tej funkcji.
- Jaką cenę płyty powinien ustalić sprzedawca, aby miesięczny zysk z jej sprzedaży był największy? Oblicz miesięczny największy zysk właściciela sklepu ze sprzedaży płyty „Emotion”.
Liczbę 7 dzielimy na trzy części tak aby pierwsza była dwa razy większa od drugiej. Jak należy dokonać podziału, aby suma kwadratów wszystkich trzech części była najmniejsza?
Suma trzech liczb rzeczywistych dodatnich jest równa 13. Druga liczba jest trzy razy większa od pierwszej. Wyznacz trzy liczby spełniające podane warunki tak, aby suma ich kwadratów była najmniejsza.
Funkcja o wzorze 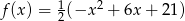 opisuje wydajność pracy robotnika w zależności od czasu pracy
opisuje wydajność pracy robotnika w zależności od czasu pracy  , w ciągu 8-godzinnego dnia pracy. Robotnik rozpoczyna pracę o godz.
, w ciągu 8-godzinnego dnia pracy. Robotnik rozpoczyna pracę o godz. 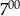 . O której godzinie jego wydajność jest największa?
. O której godzinie jego wydajność jest największa?
Firma zajmująca się wynajmem lokali ma do dyspozycji 180 pomieszczeń użytkowych. Wszystkie pomieszczenia są zajęte wówczas, gdy koszt wynajmu za jeden miesiąc wynosi 1200 zł. Firma oszacowała, że każda kolejna podwyżka czynszu o 40 zł, zmniejsza o 5 liczbę wynajmowanych pomieszczeń. Jaki miesięczny koszt wynajmu powinna ustalić ta firma, aby jej przychód był maksymalny? Ile wynosi maksymalny przychód?
Liczbę dodatnią  przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.
przedstaw w postaci sumy dwóch takich składników, aby suma ich sześcianów była najmniejsza.
- Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
- Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.
Z krawędzi dachu podrzucono kamień, który po 2 sekundach spadł na ziemię. Wysokość (wyrażoną w metrach), na jakiej znajdował się kamień nad ziemią po upływie 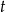 sekund od chwili jego podrzucenia, opisuje funkcja
sekund od chwili jego podrzucenia, opisuje funkcja 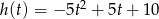 , gdzie
, gdzie 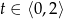 .
.
- Podaj, z jakiej wysokości (od ziemi) kamień został podrzucony.
- Oblicz, po jakim czasie od momentu podrzucenia kamień osiągnął największą wysokość.
- Oblicz największą wysokość (od ziemi), na jaką wzniósł się ten kamień.
Pewna firma komputerowa produkuje dwa typy komputerów. Koszt części potrzebnych do złożenia komputera I rodzaju wynosi 1500 zł, a II rodzaju 2000 zł. Firma zyskuje na każdym sprzedanym komputerze I typu 400 zł, a II typu 600 zł. Tygodniowo firma przeznacza na potrzebne materiały co najwyżej 32500 zł i sprzedaje 20 komputerów. Ile komputerów każdego rodzaju powinna firma produkować tygodniowo, aby zysk jej był jak największy? Jaki to będzie zysk?
Firma wynajmująca samochody ma do dyspozycji 180 pojazdów. Wszystkie samochody są wynajęte wówczas, gdy koszt wynajmu jednego samochodu za jeden tydzień wynosi 1200 zł. Właściciel firmy oszacował, że każda kolejna podwyżka ceny wynajmu samochodu o 40 zł tygodniowo powoduje zmniejszenie liczby wynajmowanych samochodów o 3. Jaki tygodniowy koszt wynajmu powinna ustalić firma, aby jej przychód był maksymalny? Ile wynosi ten największy przychód?
Wyznacz takie dwie liczby o sumie 100, których suma kwadratów jest najmniejsza.
Z murów zamku wystrzelono pocisk armatni, który po 4 sekundach spadł na ziemię. Wysokość (w metrach), na jaką wzniósł się pocisk (względem poziomu armaty) po upływie 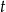 sekund od momentu wystrzelenia opisuje funkcja
sekund od momentu wystrzelenia opisuje funkcja 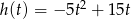 , gdzie
, gdzie 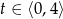 .
.
- Oblicz po jakim czasie pocisk ponownie znalazł się na wysokości z jakiej został wystrzelony.
- Oblicz na jaką maksymalną wysokość względem ziemi wzniósł się ten pocisk.
Hurtownik sprzedaje obuwie po 80 złotych za parę, o ile zamówienie jest mniejsze niż 50 par butów. Jeśli zamówienie jest nie mniejsze niż 50 par, ale nie większe niż 600 par obuwia, to wówczas cena jednej pary obuwia spada o 10 groszy pomnożone przez liczbę zamówionych par. Jaka wielkość zamówienia maksymalizuje przychód hurtownika? Ile wyniesie ten maksymalny przychód?
Sprzedawca kupuje miesięcznie w hurtowni laptopy, płacąc 1200 zł za sztukę. W chwili obecnej sprzedaje 20 laptopów miesięcznie w cenie 1400 zł za sztukę, oraz oszacował, że każda kolejna obniżka ceny o 10 zł zwiększa o 2 liczbę sprzedanych laptopów. Jaką powinien ustalić cenę laptopa, aby jego zysk był największy? Ile jest równy ten maksymalny miesięczny zysk?
Liczbę dodatnią  przedstaw w postaci sumy dwóch takich składników, aby suma ich kwadratów była najmniejsza.
przedstaw w postaci sumy dwóch takich składników, aby suma ich kwadratów była najmniejsza.
Dane są punkty 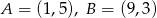 i prosta
i prosta 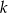 o równaniu
o równaniu 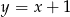 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 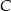 leżącego na prostej
leżącego na prostej 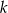 , dla którego suma
, dla którego suma 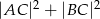 jest najmniejsza.
jest najmniejsza.
Na prostej o równaniu 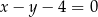 znajdź punkt
znajdź punkt 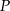 , którego kwadrat odległości od punktu
, którego kwadrat odległości od punktu 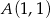 jest najmniejszy.
jest najmniejszy.
Na prostej 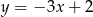 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Dwa wierzchołki prostokąta leżą na osi  , a pozostałe dwa należą do paraboli o równaniu
, a pozostałe dwa należą do paraboli o równaniu 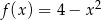 i znajdują się powyżej osi
i znajdują się powyżej osi  .
.
- Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego podstawy.
- Dla jakiej długości podstawy pole tego prostokąta jest równe 6.
- Dla jakiej długości podstawy pole tego prostokąta jest największe?
Dana jest parabola opisana równaniem 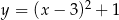 . Tworzymy trójkąty
. Tworzymy trójkąty 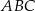 takie, że punkt
takie, że punkt 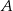 leży w początku układu współrzędnych, punkt
leży w początku układu współrzędnych, punkt 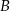 o współrzędnych
o współrzędnych 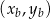 leży na paraboli, punkt
leży na paraboli, punkt 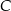 ma współrzędne
ma współrzędne 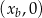 .
.
- Napisz wzór funkcji
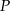 , określającej pole trójkąta
, określającej pole trójkąta 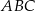 w zależności od
w zależności od 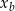 dla
dla 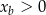 .
. - Znajdź trójkąt o największym polu dla
![xb ∈ [0;2]](https://img.zadania.info/zad/3724416/HzadT11x.gif) ; w odpowiedzi podaj współrzędne punktu
; w odpowiedzi podaj współrzędne punktu 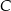 .
.
Na paraboli o równaniu 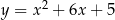 znajdź współrzędne punktu
znajdź współrzędne punktu 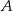 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 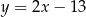 jest najmniejsza.
jest najmniejsza.
Na prostej 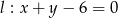 wyznacz taki punkt
wyznacz taki punkt 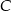 , aby długość łamanej
, aby długość łamanej 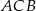 , gdzie
, gdzie 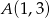 ,
, 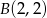 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie.
Dane są punkty 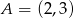 i
i 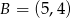 . Na prostej o równaniu
. Na prostej o równaniu 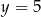 wyznacz punkt
wyznacz punkt 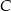 tak, aby łamana
tak, aby łamana 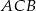 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.
Dane są punkty 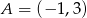 i
i 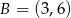 . Funkcja
. Funkcja 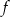 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 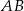 jego odległość od punktu
jego odległość od punktu 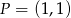 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 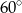 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
Wyznacz wymiary prostokąta o obwodzie 36 cm, którego pole jest największe.
W trójkąt prostokątny o przyprostokątnych długości 6 i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych, a jeden z jego wierzchołków leży na przeciwprostokątnej. Zbadaj, jakie powinny być wymiary prostokąta, aby jego pole było możliwie największe.
W trójkąt prostokątny o kącie ostrym 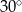 i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.
Na bokach prostokąta o obwodzie 16 cm opisano, jako na średnicach, półokręgi leżące na zewnątrz prostokąta. Zbadaj, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech półokręgów jest najmniejsze. Oblicz to pole
Wewnątrz prostokąta 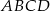 o wymiarach
o wymiarach 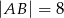 i
i 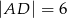 wybrano dwa punkty
wybrano dwa punkty 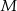 i
i 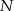 takie, że
takie, że 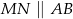 oraz
oraz 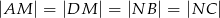 . Przy jakiej odległości punktów
. Przy jakiej odległości punktów 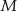 i
i 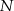 suma kwadratów długości odcinków
suma kwadratów długości odcinków 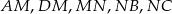 jest najmniejsza?
jest najmniejsza?
Bok kwadratu 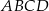 ma długość 1. Na bokach
ma długość 1. Na bokach 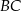 i
i 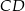 wybrano odpowiednio punkty
wybrano odpowiednio punkty 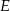 i
i 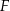 umieszczone tak, by
umieszczone tak, by 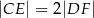 . Oblicz wartość
. Oblicz wartość 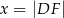 , dla której pole trójkąta
, dla której pole trójkąta 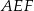 jest najmniejsze.
jest najmniejsze.
W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.
Obwód trapezu równoramiennego kącie ostrym 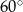 równa się
równa się 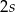 (
(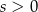 ). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
W trójkąt prostokątny 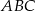 , w którym
, w którym 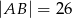 ,
, 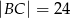 ,
, 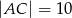 , wpisujemy prostokąty
, wpisujemy prostokąty 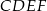 , tak, że punkt
, tak, że punkt 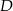 należy do boku
należy do boku 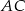 , pkt
, pkt 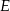 należy do boku
należy do boku 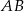 i punkt
i punkt 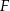 należy do boku
należy do boku 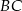 . Oblicz wymiary prostokąta o największym polu.
. Oblicz wymiary prostokąta o największym polu.
Drut o długości 28 cm należy podzielić na dwie części i z jednej zrobić kwadratową ramkę, a z drugiej ramkę prostokątną, której jeden bok jest trzy razy dłuższy od drugiego. Jak należy podzielić drut, jeżeli chcemy, aby suma pól otrzymanego kwadratu i prostokąta była najmniejsza?
Suma długości dwóch boków trójkąta jest równa 12cm, a kąt między tymi bokami ma miarę 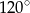 . Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
. Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
Ratownicy mający do dyspozycji linę o długości 80 metrów mają wytyczyć przy brzegu plaży kąpielisko w kształcie prostokąta (wzdłuż brzegu nie będzie liny). Jakie wymiary powinno mieć to kąpielisko, jeżeli wczasowicze chcą, aby miało ono jak największą powierzchnię? Należy przyjąć, że brzeg plaży tworzy linię prostą.

