Zestaw użytkownika nr 7687_1555
Zestaw użytkownika
nr 7687_1555
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 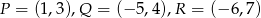 .
.
Dla jakich wartości parametru  odległość punktu
odległość punktu 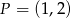 od prostej
od prostej 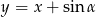 jest mniejsza lub równa
jest mniejsza lub równa 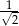 .
.
Wyznacz współrzędne punktu 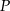 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 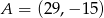 i
i 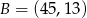 w stosunku
w stosunku 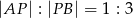 .
.
Dane są punkty 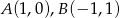 . Punkt
. Punkt 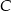 należy do okręgu o równaniu
należy do okręgu o równaniu 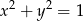 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 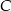 , tak aby pole trójkąta było największe. Oblicz to pole.
, tak aby pole trójkąta było największe. Oblicz to pole.
Wyznacz równanie okręgu, który jest symetryczny do okręgu o równaniu
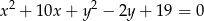
względem prostej 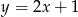 .
.
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 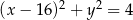 jest okrąg o równaniu
jest okrąg o równaniu 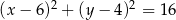 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 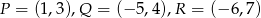 .
.
Dla jakich wartości parametru  odległość punktu
odległość punktu 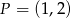 od prostej
od prostej 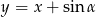 jest mniejsza lub równa
jest mniejsza lub równa 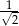 .
.
Wyznacz współrzędne punktu 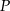 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 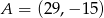 i
i 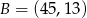 w stosunku
w stosunku 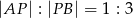 .
.
Dane są punkty 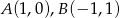 . Punkt
. Punkt 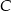 należy do okręgu o równaniu
należy do okręgu o równaniu 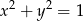 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 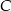 , tak aby pole trójkąta było największe. Oblicz to pole.
, tak aby pole trójkąta było największe. Oblicz to pole.
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 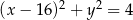 jest okrąg o równaniu
jest okrąg o równaniu 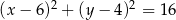 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Punkty 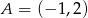 i
i 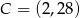 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 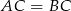 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 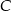 ma równanie
ma równanie 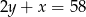 . Oblicz pole trójkąta
. Oblicz pole trójkąta 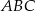 .
.
Wyznacz równanie takiej prostej przechodzącej przez punkt 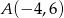 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
Który z odcinków łączących dowolny punkt paraboli o równaniu 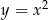 z punktem
z punktem 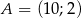 ma najmniejszy kwadrat długości?
ma najmniejszy kwadrat długości?
Napisz równanie okręgu o środku 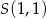 , który na prostej o równaniu
, który na prostej o równaniu 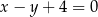 odcina cięciwę
odcina cięciwę 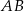 długości
długości 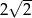 . Wykonaj rysunek.
. Wykonaj rysunek.
Kwadrat o wierzchołkach 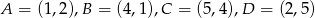 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 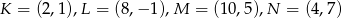 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
W trójkąt równoboczny 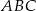 wpisano okrąg o środku w punkcie
wpisano okrąg o środku w punkcie 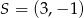 . Wiedząc, że wierzchołek
. Wiedząc, że wierzchołek 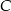 ma współrzędne
ma współrzędne 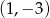 wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
Wierzchołek 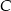 trójkąta
trójkąta 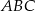 leży na okręgu o równaniu
leży na okręgu o równaniu 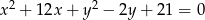 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 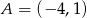 i
i 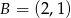 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
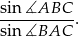
Napisz równanie okręgu opisanego na trójkącie o wierzchołkach 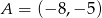 ,
, 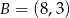 i
i 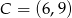 .
.
Dane są punkty 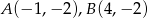 oraz
oraz 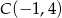 .
.
- Za pomocą odpowiedniego układu nierówności opisz trójkąt
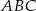 .
. - Oblicz odległość punktu
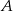 od prostej
od prostej 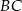 .
. - Oblicz promień koła wpisanego w trójkąt
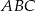 .
. - Wyznacz równanie symetralnej boku
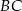 .
.
Oblicz miarę kąta między stycznymi do okręgu  poprowadzonymi przez punkt
poprowadzonymi przez punkt 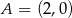 .
.
Sprawdź czy punkt 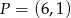 leży na dwusiecznej kąta
leży na dwusiecznej kąta 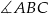 trójkąta o wierzchołkach
trójkąta o wierzchołkach 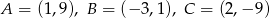 .
.
Wykaż, że cosinus kąta przecięcia się wykresów funkcji 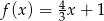 i
i 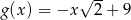 jest równy
jest równy 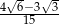 .
.

