Zestaw użytkownika nr 7704_2621

Graniastosłupy

Zadanie 1

Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 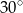30∘ . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.

Zadanie 2

Podstawą graniastosłupa jest trójkąt prostokątny równoramienny o ramieniu długości 9. Kąt między przekątną największej ściany bocznej i wysokością graniastosłupa jest równy 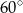60∘ . Oblicz pole powierzchni bocznej i objętość tego graniastosłupa.

Zadanie 3

Objętość graniastosłupa prawidłowego trójkątnego jest równa 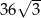√ -- 36 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.

Zadanie 4

Objętość graniastosłupa prawidłowego trójkątnego jest równa 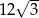√ -- 12 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.

Zadanie 5

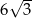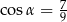Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość √ -- 6 3 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt taki, że cosα = 7 9 . Oblicz objętość graniastosłupa.

Zadanie 6

Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.

Zadanie 7

Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem 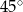45 ∘ do dolnej podstawy. Pole otrzymanego przekroju wynosi 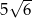√ -- 5 6 . Oblicz objętość tego graniastosłupa.

Zadanie 8

W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy 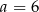a = 6 przekątna ściany bocznej tworzy z drugą ścianą boczną kąt o mierze 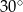30 ∘ . Oblicz

długość przekątnej ściany bocznej,
długość wysokości graniastosłupa,
objętość i pole powierzchni całkowitej.

Zadanie 9

Podstawą prostopadłościanu jest kwadrat. Przekątna tego prostopadłościanu ma długość 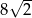√ -- 8 2 i jest nachylona do płaszczyzny podstawy pod kątem 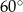60 ∘ . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.

Zadanie 10

Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 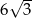√ -- 6 3 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.

Arkusz Wersja PDF