Zestaw użytkownika nr 7705_7463
Funkcja kwadratowa25 Stycznia 2012
Rozwiąż równanie: 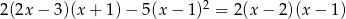 .
.
Rozwiązaniami równania 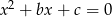 są liczby 8 i -3. Wyznacz parametry
są liczby 8 i -3. Wyznacz parametry 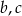 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 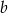 ,
,  równanie
równanie 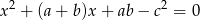 ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Funkcja kwadratowa postaci 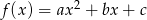 , posiada miejsca zerowe równe -3 i 2, a jej współczynnik
, posiada miejsca zerowe równe -3 i 2, a jej współczynnik 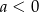 . Oblicz wartości współczynników
. Oblicz wartości współczynników 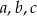 wiedząc, ze największa wartość funkcji wynosi
wiedząc, ze największa wartość funkcji wynosi 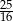 .
.
Rozwiąż graficznie i algebraicznie układ równań
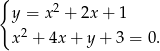
Wyznacz wszystkie liczby pierwsze spełniające nierówność
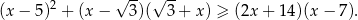
Rozwiąż nierówność 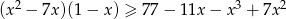 .
.
Funkcja kwadratowa 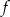 jest określona wzorem
jest określona wzorem 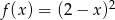 .
.
- Wyznacz najmniejszą i największą wartość funkcji
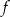 w przedziale
w przedziale 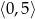 .
. - Rozwiąż nierówność
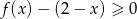 .
.
Dane są funkcje 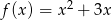 i
i 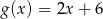 . Rozwiąż nierówność
. Rozwiąż nierówność 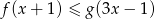 .
.
Funkcje 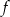 i
i 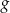 dane są wzorami
dane są wzorami 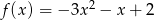 ,
, 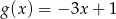 . Wyznacz zbiór argumentów
. Wyznacz zbiór argumentów  , dla których funkcja
, dla których funkcja 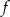 przyjmuje wartości większe od funkcji
przyjmuje wartości większe od funkcji 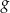 .
.
Rozwiąż nierówność 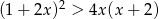 .
.
Dany jest trójmian kwadratowy 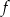 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 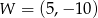 . Oblicz
. Oblicz 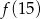 .
.
Pierwiastkami trójmianu kwadratowego 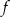 o współczynniku -3 przy najwyższej potędze są liczby
o współczynniku -3 przy najwyższej potędze są liczby 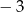 . Oblicz
. Oblicz 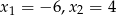 .
.
Funkcja kwadratowa 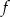 określona jest wzorem
określona jest wzorem 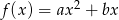 . Wiadomo, że
. Wiadomo, że 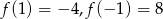 . Określ, dla jakich argumentów spełniona jest nierówność
. Określ, dla jakich argumentów spełniona jest nierówność 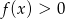 .
.
Dla jakiego 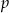 prosta o równaniu
prosta o równaniu 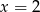 jest osią symetrii wykresu funkcji
jest osią symetrii wykresu funkcji 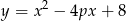 .
.
Funkcja 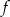 określona jest wzorem
określona jest wzorem 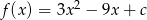 , gdzie
, gdzie 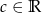 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika  , dla których:
, dla których:
- jednym z miejsc zerowych funkcji
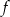 jest liczba 2;
jest liczba 2; - wierzchołek paraboli, która jest wykresem funkcji
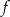 , należy do prostej o równaniu
, należy do prostej o równaniu 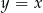 .
.
Dana jest funkcja 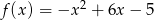 .
.
- Narysuj parabolę, która jest wykresem funkcji
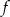 i zaznacz na rysunku współrzędne jej wierzchołka oraz punktów przecięcia paraboli z osiami układu współrzędnych.
i zaznacz na rysunku współrzędne jej wierzchołka oraz punktów przecięcia paraboli z osiami układu współrzędnych. - Odczytaj z wykresu zbiór wartości funkcji
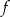 .
. - Rozwiąż nierówność
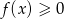 .
.