Zestaw użytkownika nr 7726_5074
PrawdopodobienstwoUrny, szuflady
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 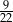 .
.
W urnie znajduję się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
W urnie jest pewna liczba kul białych i pewna liczba kul czarnych – razem 9 kul. Ile jest kul białych w urnie, jeśli wiadomo, że przy jednoczesnym losowaniu dwóch kul z tej urny prawdopodobieństwo otrzymania kul tego samego koloru jest równe prawdopodobieństwu otrzymania kul różnych kolorów?
Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe 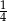 ?
?
Liczby kul białych, niebieskich i czerwonych tworzą - w podanej kolejności - ciąg arytmetyczny o różnicy 2. Spośród tych kul losujemy jednocześnie trzy. Prawdopodobieństwo wylosowania trzech kul, z których każda jest innego koloru wynosi 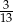 . Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.
. Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.
W jednej urnie jest 5 kul białych i pewna liczba kul czarnych, w drugiej zaś 6 kul czarnych i pewna liczba kul białych. Z każdej urny losujemy po dwie kule. Prawdopodobieństwo wylosowania jednocześnie dwóch kul białych z pierwszej urny jest większe od  , a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od
, a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od 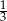 . W której urnie jest więcej kul białych, a w której czarnych?
. W której urnie jest więcej kul białych, a w której czarnych?
Z urny zawierającej 8 kul białych i 4 czarne wylosowano bez zwracania 5 kul. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowana kula jest czerwona lub zielona.
W urnie znajduje się  kul czarnych i
kul czarnych i 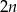 kul białych (
kul białych (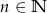 ,
, 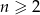 ). Losujemy jednocześnie dwie kule. Dla jakich
). Losujemy jednocześnie dwie kule. Dla jakich  prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?
prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?
W urnie znajduje się 27 kul w dwóch kolorach. Wiadomo, że wśród każdych 13 kul wybranych z urny jest co najmniej jedna czarna, a wśród każdych 16 kul jest co najmniej jedna biała. Ile białych kul znajduje się w urnie?
W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi 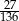 . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.
. Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.
W urnie są 3 kule białe, 4 czarne i 5 zielonych. Losujemy ze zwracaniem 3 kule. Oblicz prawdopodobieństwo tego, że wśród wylosowanych kul będą kule biała i czarna.
W urnie jest 15 kartek, ponumerowanych liczbami od 1 do 15. Wyciągamy 5 kartek bez zwracania. Jakie jest prawdopodobieństwo, że numer trzeciej kartki jest liczbą podzielną przez 3 i jednocześnie numer piątej kartki jest liczbą podzielną przez 5?
W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia 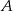 – wylosowano trzy kule tego samego koloru;
– wylosowano trzy kule tego samego koloru;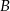 – żadne dwie z wylosowanych kul nie są tego samego koloru.
– żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia 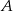 jeżeli prawdopodobieństwo zdarzenia
jeżeli prawdopodobieństwo zdarzenia 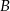 jest równe
jest równe 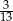 .
.
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej.
W urnie znajdują się kule białe, zielone i czerwone. Kul zielonych jest dwa razy więcej niż kul białych, a kul czerwonych jest 3 razy więcej niż białych. Wyjęto dwa razy po jednej kuli bez zwracania. Oblicz liczbę kul białych w urnie, jeśli prawdopodobieństwo wylosowania dwóch kul zielonych jest równe 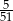 .
.
Z urny, w której znajduje się 20 kul białych i 2 czarne losujemy  kul. Znajdź najmniejszą wartość
kul. Znajdź najmniejszą wartość  , taką przy której prawdopodobieństwo wylosowania przynajmniej jednej kuli czarnej jest większe od
, taką przy której prawdopodobieństwo wylosowania przynajmniej jednej kuli czarnej jest większe od 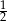 .
.
Co czwarta kula w urnie to biała, pozostałe mają kolor czarny lub niebieski. Losujemy jedna kulę. Prawdopodobieństwo wylosowania kuli niebieskiej lub białej jest dwukrotnie mniejsze niż prawdopodobieństwo wylosowania kuli niebieskiej lub czarnej. Oblicz prawdopodobieństwo wylosowania kuli czarnej.
W urnie znajduje się 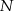 losów, przy czym
losów, przy czym 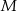 z nich to losy wygrywające (
z nich to losy wygrywające (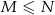 ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (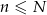 ) i niech
) i niech 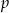 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 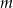 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (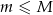 oraz
oraz 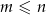 ). Uzasadnij, że
). Uzasadnij, że
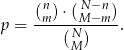
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 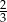 ?
?
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
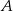 – wszystkie kule znajdą się w szufladach z numerami parzystymi.
– wszystkie kule znajdą się w szufladach z numerami parzystymi. 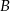 – dokładnie dwie szuflady pozostaną puste.
– dokładnie dwie szuflady pozostaną puste.
W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.
- Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
- Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
- Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?
Rozmieszczamy 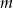 różnych listów w
różnych listów w 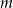 rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
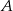 – co najmniej jedna skrytka jest pusta?
– co najmniej jedna skrytka jest pusta? 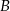 – co najmniej dwie skrytki są puste?
– co najmniej dwie skrytki są puste?
W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe?
Rozmieszczamy 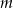 różnych listów w
różnych listów w 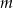 rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?
rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?
Do 12 ponumerowanych szuflad wkładamy losowo 13 pojedynczych skarpetek, przy czym dokładnie dwie z nich tworzą parę. Jakie jest prawdopodobieństwo otrzymania konfiguracji, w której żadna szuflada nie jest pusta oraz skarpetki tworzące parę znajdują się w różnych szufladach.
10 kul rozmieszczamy w 10 szufladach. Jakie jest prawdopodobieństwo tego, że każda szuflada będzie zajęta?
W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:
- wylosujemy dwa klocki białe;
- wylosujemy klocki tego samego koloru.
Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobieństwo, że przynajmniej dwa listy znajdą się w tej samej skrzynce?
Na stole stoją dwa identyczne koszyki, w których znajduje się po 15 jednakowej wielkości piłeczek. Piłeczki są w kolorze żółtym i czerwonym. W obu koszykach liczba piłeczek żółtych jest taka sama. Z każdego koszyka losujemy jedną piłeczkę. Ile powinno być w każdym koszyku żółtych piłeczek, aby prawdopodobieństwo wylosowania piłeczek różnych kolorów było największe?
W pojemniku znajduje się 28 kul, przy czym  z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby  prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
W jednej szufladzie znajduje się 6 czapek: 3 zielone, 2 czerwone i 1 niebieska, a w drugiej szufladzie jest 7 szalików: 2 zielone, 1 czerwony i 4 niebieskie. Wyjęto losowo jedną czapkę i jeden szalik. Oblicz prawdopodobieństwo zdarzenia A – wylosowana czapka i wylosowany szalik są tego samego koloru.
Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe , 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.
Z szuflady, w której znajduje się 10 różnych par rękawiczek wybieramy losowo cztery rękawiczki. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwa zdarzeń:
A – wśród wylosowanych rękawiczek nie będzie pary,
B – wśród wylosowanych rękawiczek będzie dokładnie jedna para.

