Zestaw użytkownika nr 7753_1025
Zestaw użytkownika
nr 7753_1025
Spośród liczb 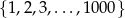 losujemy jednocześnie dwie, które oznaczamy
losujemy jednocześnie dwie, które oznaczamy  i
i 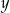 . Ile jest możliwości wylosowania takiej pary liczb
. Ile jest możliwości wylosowania takiej pary liczb 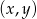 , dla której:
, dla której:
 jest podzielne przez 23, a
jest podzielne przez 23, a 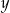 nie jest podzielne przez 23?
nie jest podzielne przez 23? 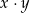 jest podzielne przez 23?
jest podzielne przez 23?
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest parzysta, a pozostałe nieparzyste.
Z elementów zbioru 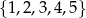 losujemy kolejno ze zwracaniem trzy:
losujemy kolejno ze zwracaniem trzy: 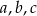 . Ile mamy możliwości wylosowania takiej trójki, aby utworzyła ona:
. Ile mamy możliwości wylosowania takiej trójki, aby utworzyła ona:
- ciąg arytmetyczny niemalejący?
- ciąg arytmetyczny?
- ciąg geometryczny?
Ile jest liczb naturalnych czterocyfrowych, w których żadne dwie spośród cyfr: 1,3,5,7,9 nie sąsiadują ze sobą?
Ze zbioru 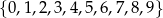 losujemy kolejno 4 cyfry bez zwracania, a następnie zapisujemy je w kolejności losowania tworząc liczbę 4 cyfrową. Ile można otrzymać w ten sposób
losujemy kolejno 4 cyfry bez zwracania, a następnie zapisujemy je w kolejności losowania tworząc liczbę 4 cyfrową. Ile można otrzymać w ten sposób
- dowolnych liczb?
- liczb podzielnych przez 25?
Ile można utworzyć trójkątów równoramiennych, których wierzchołki są jednocześnie wierzchołkami ustalonego dziesięciokąta foremnego?
Z talii 52 kart losujemy bez zwracania 8 kart. Ile jest możliwych wyników losowania, w których są dokładnie 2 walety i 4 damy.
Ile jest liczb naturalnych ośmiocyfrowych, których suma cyfr jest równa 4?
Cyfry 0, 1, 2, 3, 4, 5, 6 ustawiamy losowo w liczbę siedmiocyfrową, której pierwsza cyfra nie jest równa 0. Ile jest możliwych ustawień, w których otrzymamy liczbę siedmiocyfrową
- podzielną przez 4
- parzystą.
Na jednej prostej zaznaczono 3 punkty, a na drugiej 4 punkty.
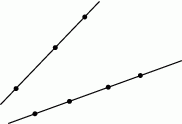
Ile jest wszystkich trójkątów, których wierzchołkami są trzy spośród zaznaczonych punktów?
Ile jest liczb naturalnych czterocyfrowych takich, że w ich zapisie dziesiętnym występuje jedna cyfra nieparzysta i trzy cyfry parzyste?
Uwaga: przypominamy, że zero jest liczbą parzystą.
Ile jest liczb dziewięciocyfrowych, w których suma każdych trzech kolejnych cyfr jest równa 10?
Ile liczb parzystych, trzycyfrowych, o różnych cyfrach można utworzyć z elementów zbioru 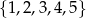 ?
?
W turnieju karate rozegrano 36 walk. Każdy walczył z każdym dokładnie raz. Ilu zawodników brało udział w turnieju?
Wyznacz liczbę  , wiedząc że
, wiedząc że 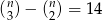 .
.
W torebce znajduje się 5 cukierków miętowych i 6 owocowych. Z torebki losujemy 4 cukierki. Na ile sposobów można wylosować 2 cukierki miętowe i 2 owocowe?
Ile jest takich czwórek liczb całkowitych i dodatnich 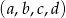 , które spełniają równanie
, które spełniają równanie 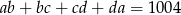 .
.
Ile można utworzyć różnych wyrazów mających sens lub nie z wszystkich liter wyrazu:
- ’permutacje’.
- ’internet’;
Ze zbioru 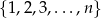 , gdzie
, gdzie 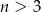 losujemy bez zwracania dwie liczby. Oznaczmy je, w kolejności losowania przez
losujemy bez zwracania dwie liczby. Oznaczmy je, w kolejności losowania przez  i
i 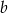 . Ile jest możliwości wylosowania:
. Ile jest możliwości wylosowania:
- dowolnej pary liczb?
- pary liczb, dla której
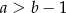 ?
? - pary liczb, dla której
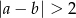 ?
?
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Ze zbioru liczb 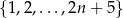 wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
wybieramy jednocześnie dwie liczby (nie uwzględniamy kolejności). Na ile sposobów możemy to zrobić, tak aby otrzymać dwie liczby takie, że:
- ich różnica będzie liczbą parzystą,
- suma ich kwadratów będzie liczbą podzielną przez cztery?
Z cyfr 1,2,3,4,5,6,7,8 tworzymy liczby sześciocyfrowe. Ile można utworzyć takich liczb w których cyfra 1 występuje co najmniej trzy razy, a pozostałe cyfry są różne między sobą?
W barze są do wyboru: 4 zupy, 5 drugich dań i 3 desery. Ile różnych dań obiadowych złożonych z zupy, drugiego dania i deseru można zamówić w tym barze? (Za różne uważamy zestawy, które różnią się przynajmniej jednym elementem).
Oblicz, ile jest liczb ośmiocyfrowych, w zapisie których nie występuje zero, natomiast występują dwie dwójki i występują trzy trójki.
Oblicz, ile jest liczb naturalnych czterocyfrowych, które są podzielne przez 5, i których zapis składa się z 4 różnych cyfr.
Iloma sposobami można umieścić 20 kul w szufladach tak, aby w pierwszej było 10, w drugiej 6, a w trzeciej 4?
Ile jest liczb pięciocyfrowych, spełniających jednocześnie następujące cztery warunki:
(1) cyfry setek, dziesiątek i jedności są parzyste,
(2) cyfra setek jest większa od cyfry dziesiątek,
(3) cyfra dziesiątek jest większa od cyfry jedności,
(4) w zapisie tej liczby nie występuje cyfra 9.
Z urny, w której jest 15 losów, w tym 5 wygrywających, wyciągamy 3 losy. Na ile sposobów można wylosować?
- same losy wygrywające?
- dokładnie 1 los wygrywający?
- co najmniej 2 losy wygrywające?
Okrąg podzielono dwudziestoma punktami na dwadzieścia łuków tej samej długości. Ile można zbudować łamanych zamkniętych z wierzchołkami w tych punktach i z odcinkami równej długości? (Odcinki mogą się przecinać, ale nie mogą się pokrywać.)
Wyznacz wszystkie liczby naturalne  spełniające równanie
spełniające równanie
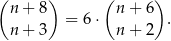
Ze zbioru 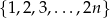 , gdzie
, gdzie 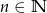 , losujemy jednocześnie trzy liczby. Ile mamy możliwości wylosowania takich trzech liczb, których suma jest nieparzysta?
, losujemy jednocześnie trzy liczby. Ile mamy możliwości wylosowania takich trzech liczb, których suma jest nieparzysta?
Ile jest liczb naturalnych trzycyfrowych, w których cyfra dziesiątek jest o 2 większa od cyfry jedności?
Rozwiąż równanie 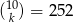 .
.
Oblicz ile liczb podzielnych przez 7 znajduje się w przedziale 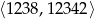 .
.

