Zestaw użytkownika nr 7832_6969
Zestaw użytkownika
nr 7832_6969
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?
Wnuczek ma tyle miesięcy co dziadek lat. Razem maja 91 lat. Ile lat ma dziadek, a ile wnuczek?
Ciocia jest 3 razy starsza od Basi. Za 16 lat Basia będzie miała tyle lat, ile ciocia przed 6 laty. Ile lat obecnie ma ciocia, a ile Basia?
Ojciec i córka mają razem 50 lat. Pięć lat temu ojciec był 9 razy starszy od córki. Ile lat ma obecnie każde z nich.
Dwa lata temu córka była 6 razy młodsza od matki, a za cztery lata matka będzie 3 razy starsza od córki. Ile lat ma teraz córka?
Za 4 jednakowe swetry i spodnie zapłacono 384 zł, a za sam sweter i spodnie 132 zł. Ile kosztuje sweter, a ile spodnie?
Pani Kowalska pobrała w banku kwotę 1000 zł w banknotach 20 zł i 50 zł. Łącznie otrzymała 32 banknoty. Ile otrzymała banknotów każdego rodzaju?
Do sklepu warzywno-owocowego zakupiono w hurtowni 250 kg pomidorów za 800 zł. Pierwszego dnia sprzedano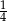 
ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia 
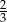tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
Gdyby 4 osboby przeszły z partii Cymbałków do partii Trąbek, obie partie liczyłyby tyle samo członków. Gdyby z partii Trąbek 4 osoby przeszły do partii Cymbałków, to w Cymbałkach byłoby 3 razy więcej członków niż w Trąbkach. Ile osób należy do partii Trąbek?
Liczby mieszkańców (w przybliżeniu) Polski, Czech i Słowacji są w stosunku 390:103:54. Różnica liczb mieszkańców w Czechach i Słowacji jest równa 4,9 mln osób. Ilu mieszkańców jest w każdym z tych krajów?
W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.
Suma trzech liczb jest równa 2520. Jakie to liczby jeżeli ich stosunek jest równy 4:5:9?
Suma cyfr pewnej liczby dwucyfrowej wynosi 9. Jeśli między cyfrę dziesiątek a cyfrę jedności wstawimy zero, to otrzymamy liczbę o 90 większą. Jaka to liczba?
Znajdź liczbę dwucyfrową wiedząc, że suma cyfr dziesiątek i jedności tej liczby jest równa 7, zaś różnica między szukaną liczbą i liczbą o tych samych cyfrach, lecz napisanych w odwrotnym porządku jest równa 27.
Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?
Trasa rowerowa wokół jeziora ma długość 15 km. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro poruszając się w tym samym kierunku. Średnia prędkość drugiego z nich jest większa od średniej prędkości pierwszego o 5 km/h. Oblicz po jakim czasie dojdzie do ponownego spotkania rowerzystów.
Motocyklista i rowerzysta jeżdżą po zamkniętym torze w tym samym kierunku. Motocyklista dubluje rowerzystę co 25 s. Z jaką prędkością jedzie każdy z nich, jeśli motocyklista jedzie 3 razy szybciej od rowerzysty, a tor ma długość 400 m?
Przy jednoczesnej pracy 40 identycznych pomp nadmuchowych, żądany przepływ powietrza można zrealizować w ciągu 24 godzin. W ciągu ilu godzin można zrealizować ten sam przepływ powietrza przy jednoczesnej pracy 60 pomp?
Najmniejszym ssakiem na Ziemi jest ryjówka etruska. Najmniejszy zbadany osobnik ważył 2 g. Jego ogon miał 2,5 cm długości i stanowił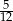 
długości całego ciała. Jaką długość miało ciało ryjówki?
Asi zerwał się naszyjnik. Trzecią część korali znalazła na podłodze, jedna czwarta w kieszeni, jedna piąta pod oparciem kanapy, a szósta część korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku?
W trzech sadach wiśniowych rosła pewna liczba drzew. W pierwszym sadzie znajdowało się 
, a w drugim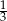 
wszystkich drzew. W trzecim rosło 320 drzew. Ile drzew rosło w każdym sadzie?
Ojciec podzielił w testamencie swój majątek pomiędzy trzech synów w ten sposób, że najstarszy miał dostać dwa razy więcej majątku niż średni, zaś średni - dwa razy więcej niż najmłodszy syn. Jaką część majątku otrzymał najmłodszy syn?
Dwudziestu sześciu uczniów klasy gimnazjalnej postanowiło wybrać się na czterodniową wycieczkę z trzema noclegami. Trasa przejazdu wynosiła łącznie 600 km. W biurze turystycznym uczniowie otrzymali następujące propozycje:
– cena jednego noclegu – 25 zł od osoby
– wyżywienie w ciągu jednego dnia (śniadanie, obiad, kolacja) – 30 zł od osoby
– bilety wejściowe do muzeum i przewodnik grupy dla całej wycieczki – 1200 zł
– cena 1 km przejazdu autokarem – 2,50 zł
Oblicz łączny koszt wycieczki dla całej grupy, jeśli pierwszego dnia uczniowie mają zamiar skorzystać tylko z obiadu i kolacji, czwartego dnia tylko ze śniadania. Oblicz koszt wycieczki na jednego ucznia.
Piotrek kupił 3 rodzaje ciastek: duże, średnie i małe. Duże ciastko kosztuje 4 zł za sztukę, średnie po 2 zł, a małe po 1zł. Piotrek kupił łącznie 10 ciastek za które zapłacił 16 zł. Ile kupił dużych ciastek?
