Zestaw użytkownika nr 7845_9934

Zestaw użytkownika
nr 7845_9934

Zadanie 1
(5 pkt)

Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.

Zadanie 2
(5 pkt)

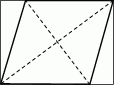
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?

PIC

Zadanie 3
(5 pkt)

W roku 2005 na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli swój wiek sprzed 10 lat pomnożę przez swój wiek za 11 lat, to otrzymam rok mojego urodzenia". Ułóż odpowiednie równanie, rozwiąż je i zapisz, w którym roku urodził się ten jubilat.

Zadanie 4
(5 pkt)

Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 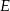E . Z punktu 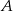A widziała ją pod kątem 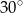30∘ stopni do kierunku drogi. A z punktu 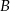B pod kątem 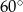60∘ . Przejeżdżając przez punkt 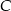C minęła elektrownię. Długość odcinka 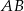AB jest równa 20km.

PIC

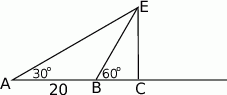
  • Oblicz miary kątów 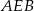AEB i BEC .
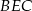  • Oblicz długość odcinka BC .
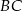  • Oblicz odległość elektrowni od drogi.

W rachunkach przyjmij, że 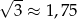√ -- 3 ≈ 1,75 .

Zadanie 5
(5 pkt)

Suma dwóch liczb równa jest 6. Znajdź te liczby, jeśli wiadomo, że suma podwojonego kwadratu jednej z nich i kwadratu drugiej jest najmniejsza z możliwych.

Zadanie 6
(5 pkt)

Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.

Zadanie 7
(5 pkt)

Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?

Zadanie 8
(5 pkt)

Wazon ma kształt sześcianu, w którym wydrążony jest walec w taki sposób, że styczne górnej podstawy walca, równoległe do odpowiednich krawędzi górnej podstawy sześcianu, są odległe o 1 cm od tych krawędzi; natomiast odległość między dolną podstawą walca, a dolną podstawą sześcianu (grubość dna) jest równa 2 cm.

PIC

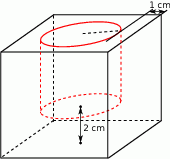
Wiedząc, że stosunek objętości walca do objętości sześcianu jest równy 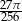272π56 , oblicz

  • długość krawędzi sześcianu;
  • objętość walca;
  • do jakiej wysokości wazonu (licząc od dolnej podstawy walca) będzie sięgać poziom wody, jeśli wlejemy do wazonu 125 ml wody. Wynik podaj z dokładnością do 1 mm.
Zadanie 9
(5 pkt)

Suma stu kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 2 wynosi 30950. Wyznacz najmniejszą i największą z tych liczb.

Zadanie 10
(5 pkt)

Zbiornik wodny o objętości 14700 litrów napełniono w całości wodą w następujący sposób. W ciągu pierwszej godziny nalano 800 litrów wody, a w ciągu każdej kolejnej godziny nalewano o 10 litrów mniej. Przez ile godzin napełniano zbiornik?

Zadanie 11
(5 pkt)

Mamy dwa pojemniki: pierwszy ma kształt sześcianu, drugi - ostrosłupa prawidłowego czworokątnego. Przekątna sześcianu ma długość 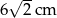√ -- 6 2 cm . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 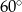60∘ . Pole powierzchni bocznej ostrosłupa jest równe 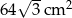√ -- 2 64 3 cm . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.

Zadanie 12
(5 pkt)

Suma kwadratów trzech kolejnych liczb naturalnych wynosi 149. Wyznacz te liczby.

Zadanie 13
(5 pkt)

W dwóch naczyniach jest woda. Gdyby z pierwszego naczynia przelano do drugiego 2 litry wody, to w obu naczyniach byłoby jej tyle samo. Gdyby zaś z drugiego do pierwszego przelano 3 litry wody, to w pierwszym naczyniu byłoby jej sześć razy więcej niż w drugim. Ile jest wody w obu naczyniach?

Zadanie 14
(5 pkt)

W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.

Zadanie 15
(5 pkt)

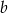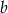Znajdź liczby a i b wiedząc, że suma liczby a i potrojonej liczby b jest równa 36, a iloczyn liczb a i b jest największy z możliwych.

Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze