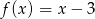Zestaw użytkownika nr 7846_1303
Zestaw użytkownika
nr 7846_1303
Napisz wzór funkcji liniowej o współczynniku kierunkowym 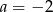 , której wykres przecina oś
, której wykres przecina oś 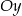 w punkcie
w punkcie 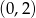 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Wyznacz wzór funkcji liniowej o współczynniku kierunkowym 2 i przechodzącej przez punkt 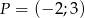 .
.
Funkcja liniowa 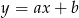 jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia
jest malejąca i jej miejscem zerowym jest liczba niedodatnia. Ustal znak wyrażenia 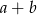 .
.
Funkcja liniowa 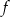 określona jest wzorem
określona jest wzorem 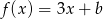 , dla
, dla 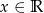 . Wyznacz współczynnik
. Wyznacz współczynnik 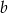 , wiedząc, że
, wiedząc, że 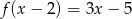 .
.
Wyznacz wzór funkcji liniowej 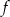 , wiedząc że nie przyjmuje ona wartości dodatnich oraz
, wiedząc że nie przyjmuje ona wartości dodatnich oraz 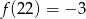 .
.
Wyznacz wzór funkcji liniowej 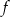 , która dla każdego
, która dla każdego 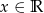 spełnia warunek
spełnia warunek 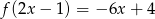 .
.
Określ wzajemne położenie prostych 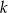 i
i 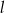 o równaniach
o równaniach
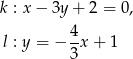
Wyznacz równanie prostej równoległej do prostej 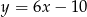 przechodzącej przez punkt
przechodzącej przez punkt 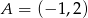 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 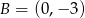 .
.
Określ wzajemne położenie prostych 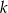 i
i 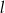 o równaniach
o równaniach
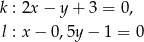
Określ wzajemne położenie prostych 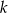 i
i 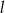 o równaniach
o równaniach
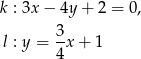
Proste o równaniach 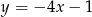 i
i 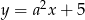 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Dane są proste o równaniach 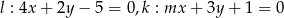 . Wyznacz parametr
. Wyznacz parametr 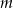 , tak aby te proste były prostopadłe.
, tak aby te proste były prostopadłe.
Dana jest funkcja 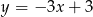 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 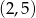 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
Określ wzajemne położenie prostych
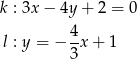
Zapisz równanie prostej przechodzącej przez punkt 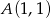 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 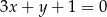 .
.
Wskaż 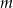 , dla którego funkcja liniowa
, dla którego funkcja liniowa 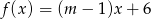 jest rosnąca
jest rosnąca
A) 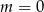 B)
B) 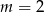 C)
C) 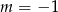 D)
D) 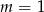
Funkcja 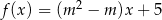 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 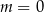 B)
B) 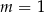 C)
C) 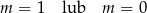 D)
D) 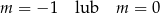
Funkcja 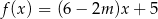 jest rosnąca, gdy
jest rosnąca, gdy
A) 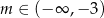 B)
B) 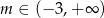 C)
C) 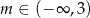 D)
D) 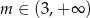
Dana jest funkcja 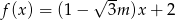 . Funkcja ta jest malejąca dla
. Funkcja ta jest malejąca dla
A) 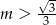 B)
B) 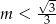 C)
C) 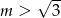 D)
D) 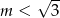
Funkcją malejącą jest funkcja
A) 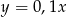 B)
B) 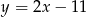 C)
C) 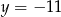 D)
D) 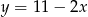
Wskaż 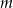 , dla którego funkcja liniowa
, dla którego funkcja liniowa 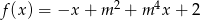 jest malejąca.
jest malejąca.
A) 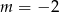 B)
B) 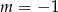 C)
C) 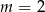 D)
D) 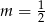
Dana jest funkcja liniowa określona wzorem 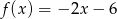 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 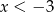 B)
B) 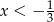 C)
C) 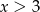 D)
D) 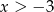
Funkcja 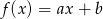 dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
A) 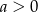 B)
B) 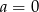 C)
C) 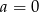 i
i 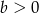 D)
D) 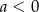
Argument funkcji 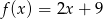 wzrasta o 5. Wówczas wartość funkcji wzrasta o
wzrasta o 5. Wówczas wartość funkcji wzrasta o
A) 10 B) 24 C) 14 D) 4
Funkcje 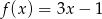 i
i 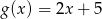 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 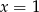 B)
B) 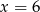 C)
C) 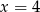 D)
D) 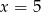
Dane są dwie funkcje liniowe określone wzorami 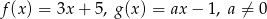 . Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
. Funkcje te mają wspólne miejsce zerowe. Wynika stąd, że
A) 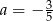 B)
B) 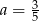 C)
C) 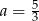 D)
D) 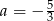
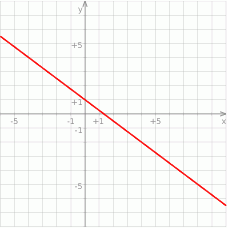
Na rysunku przedstawiony jest wykres funkcji liniowej 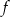 .
.
Funkcja  jest określona wzorem
jest określona wzorem
A) 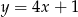 B)
B) 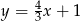 C)
C) 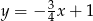 D)
D) 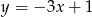
Do wykresu funkcji 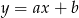 należą punkty
należą punkty 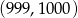 oraz
oraz 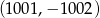 . Wówczas
. Wówczas
A) 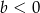 B)
B) 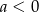 C)
C) 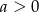 D)
D) 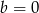
Wykresy funkcji 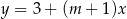 i
i 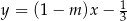 są prostopadłe. Zatem
są prostopadłe. Zatem 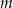
A) jest liczbą ujemną
B) jest liczbą naturalną
C) jest liczbą wymierną
D) jest liczbą niewymierną
Jeżeli wykres funkcji 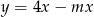 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 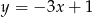 to
to
A) 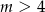 B)
B) 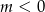 C)
C) 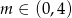 D)
D) 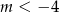
Wykres funkcji liniowej 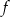 jest prostopadły do prostej
jest prostopadły do prostej 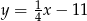 i przechodzi przez punkt
i przechodzi przez punkt 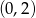 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) -8 B) -0,5 C) 0,5 D) 2
Punkt 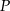 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 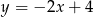 i
i 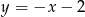 . Punkt
. Punkt 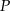 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) drugiej B) trzeciej C) pierwszej D) czwartej
Wskaż funkcję, której wykres przecina prostą o równaniu 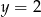 w punkcie o dodatnich współrzędnych.
w punkcie o dodatnich współrzędnych.
A) 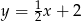 B)
B) 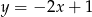 C)
C) 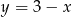 D)
D) 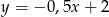
Dana jest funkcja liniowa 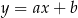 , o której wiadomo, że
, o której wiadomo, że 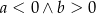 . Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
. Wykres tej funkcji przechodzi przez następujące ćwiartki układu współrzędnych
A) II, III, IV B) I, III, IV C) I, II, III D) I, II, IV
Funkcja liniowa, której wykres jest równoległy do wykresu funkcji 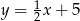 ma wzór:
ma wzór:
A) 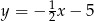 B)
B) 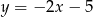 C)
C) 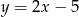 D)
D) 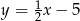
Wykres funkcji liniowej określonej wzorem 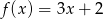 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 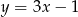 B)
B) 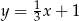 C)
C) 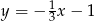 D)
D) 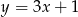
Punkt 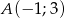 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 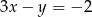 B)
B) 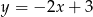 C)
C) 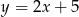 D)
D) 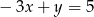
Do wykresu funkcji liniowej 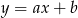 należą punkty
należą punkty 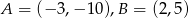 . Wynika stąd, że
. Wynika stąd, że
A) 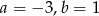 B)
B) 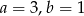 C)
C) 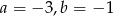 D)
D) 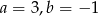
Do wykresu funkcji liniowej 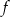 należą punkty
należą punkty 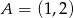 i
i 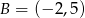 . Funkcja
. Funkcja 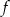 ma wzór
ma wzór
A) 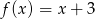 B)
B) 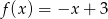 C)
C) 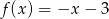 D)
D)