Zestaw użytkownika nr 7890_2304

Zestaw użytkownika
nr 7890_2304

Zadanie 1
(4 pkt)

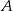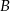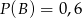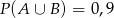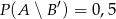O zdarzeniach A i B wiadomo, że P (B) = 0,6 , P(A ∪ B) = 0 ,9 oraz P (A ∖ B′) = 0,5 . Oblicz prawdopodobieństwo zdarzenia A .

Zadanie 2
(6 pkt)

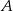W urnie jest 7 kul czarnych i 5 białych. Sześć z nich przekładamy do drugiej urny, początkowo pustej, i z niej losujemy 2 kule bez zwracania. Jakie jest prawdopodobieństwo, że druga z nich będzie biała.

Zadanie 3
(5 pkt)

W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 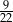-9 22 .

Zadanie 4
(4 pkt)

W zbiorze 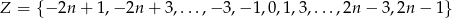Z = {− 2n + 1,− 2n + 3,...,− 3,− 1,0,1,3,...,2n − 3,2n − 1} , gdzie 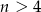n > 4 jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi 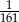1-- 161 . Wyznacz n .

Zadanie 5
(4 pkt)

Ze zbioru liczb 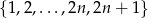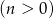{1,2,...,2n ,2n + 1} , (n > 0) , losujemy jednocześnie dwie liczby. Niech 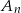An oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.

Zadanie 6
(6 pkt)

W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe 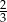2 3 ?

Zadanie 7
(4 pkt)

Ze zbioru 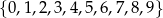{0,1,2,3,4,5,6 ,7 ,8,9} losujemy kolejno 4 cyfry bez zwracania, a następnie zapisujemy je w kolejności losowania tworząc liczbę 4 cyfrową. Ile można otrzymać w ten sposób

  • dowolnych liczb?
  • liczb podzielnych przez 25?
Zadanie 8
(3 pkt)

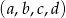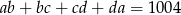Ile jest takich czwórek liczb całkowitych i dodatnich (a,b,c,d) , które spełniają równanie ab + bc + cd + da = 1004 .

Zadanie 9
(6 pkt)

Ile jest liczb naturalnych czterocyfrowych takich, że w ich zapisie dziesiętnym występuje jedna cyfra nieparzysta i trzy cyfry parzyste?
Uwaga: przypominamy, że zero jest liczbą parzystą.

Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze