Zestaw użytkownika nr 7960_5958

Zestaw użytkownika
nr 7960_5958

Zadanie 1
(5 pkt)

Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 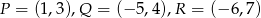P = (1,3),Q = (− 5,4),R = (− 6,7) .

Zadanie 2
(5 pkt)

Określ liczbę pierwiastków równania 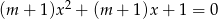2 (m + 1 )x + (m + 1)x + 1 = 0 w zależności od wartości parametru 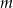m , a następnie naszkicuj wykres funkcji:

( |{ x1 + x2 gdy dane równanie ma dwa pierwiastki x1 i x2, f(m ) = |( 2x0 gdy dane równanie ma jeden pierwiastek x 0, 3− m gdy dane równanie nie ma pierwiastków .
Zadanie 3
(5 pkt)

Na rysunku przedstawiony jest wykres funkcji 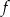f określonej wzorem 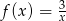f (x) = 3x dla x ⁄= 0 .

PIC

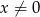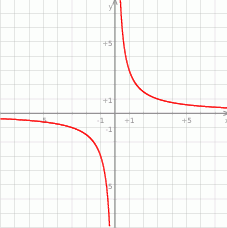
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 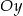Oy . Otrzymano w ten sposób wykres funkcji 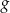g o wzorze 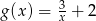g(x) = 3x + 2 dla x ⁄= 0 .

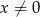  • Narysuj wykres funkcji g .
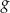  • Oblicz największą wartość funkcji 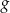g w przedziale ⟨21,31⟩ .
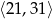  • Podaj, o ile jednostek wzdłuż osi 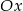Ox należy przesunąć wykres funkcji 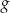g , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Zadanie 4
(5 pkt)

Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.

Zadanie 5
(5 pkt)

Dany jest wielomian 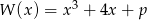3 W (x) = x + 4x + p , gdzie 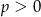p > 0 jest liczbą pierwszą. Znajdź 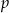p wiedząc, że 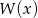W (x) ma pierwiastek całkowity.

Zadanie 6
(5 pkt)

Dana jest funkcja 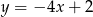y = − 4x+ 2 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor → v = [2,0] . Narysuj oba wykresy.

Zadanie 7
(5 pkt)

W roku 2005 na uroczystości urodzin zapytano jubilata, ile ma lat. Jubilat odpowiedział: „Jeśli swój wiek sprzed 10 lat pomnożę przez swój wiek za 11 lat, to otrzymam rok mojego urodzenia". Ułóż odpowiednie równanie, rozwiąż je i zapisz, w którym roku urodził się ten jubilat.

Zadanie 8
(5 pkt)

Napisz wzór funkcji liniowej o współczynniku kierunkowym 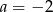a = − 2 , której wykres przecina oś 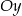Oy w punkcie 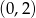(0 ,2) . Wyznacz miejsce zerowe tej funkcji.

Zadanie 9
(5 pkt)

Dane są funkcje 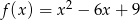2 f(x) = x − 6x+ 9 i g(x) = x + 7 .

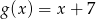  • Znajdź te argumenty, dla których zarówno funkcja 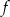f , jak i funkcja 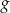g przyjmują wartości dodatnie.
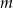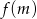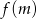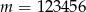  • Uzasadnij, że dla każdej liczby całkowitej m liczba f(m ) jest kwadratem liczby całkowitej. Kwadratem jakiej liczby naturalnej jest f(m ) , jeżeli m = 1234 56 ?
Zadanie 10
(5 pkt)

Romb o kącie ostrym 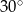∘ 30 jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.

Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze