Zestaw użytkownika nr 8000_6423
próbna matura podstawowa dla klasy 2
Liczbę 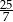 zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
zaokrąglamy do liczby 3,6. Błąd względny tego przybliżenia jest równy
A) 0,8% B) 8% C) 0,008% D) 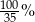
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 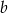 . O ile procent liczba
. O ile procent liczba 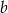 jest większa od liczby
jest większa od liczby  ?
?
A) 120% B) 25% C) 80% D) 20%
Wyrażenie 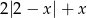 dla
dla 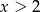 ma wartość
ma wartość
A) 1 B) 5 C) 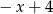 D)
D) 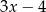
Zbiorem wszystkich rozwiązań równania 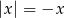 jest
jest
A) 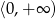 B)
B) 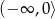 C)
C) 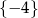 D)
D) 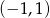
Po wykonaniu działań w wyrażeniu 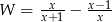 otrzymujemy
otrzymujemy
A) 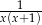 B)
B) 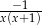 C)
C) 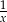 D)
D) 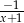
Wyrażenie 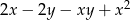 jest równe wyrażeniu
jest równe wyrażeniu
A) 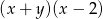 B)
B) 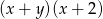 C)
C) 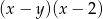 D)
D) 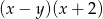
Liczba 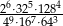 jest równa
jest równa
A) 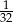 B)
B) 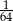 C) 32 D) 64
C) 32 D) 64
Funkcja 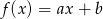 dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
dla ujemnych argumentów przyjmuje wartości ujemne, a dla dodatnich argumentów wartości dodatnie. Wynika stąd, że:
A) 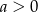 B)
B) 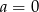 C)
C) 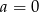 i
i 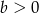 D)
D) 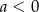
Zbiorem wartości funkcji kwadratowej 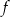 określonej wzorem
określonej wzorem 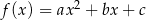 jest przedział
jest przedział 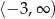 , a rozwiązaniem nierówności
, a rozwiązaniem nierówności 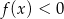 jest przedział
jest przedział 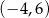 . Wskaż wzór funkcji
. Wskaż wzór funkcji 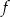 .
.
A) 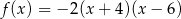
B) 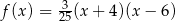
C) 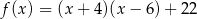
D) 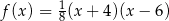
Funkcja 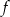 określona jest wzorem
określona jest wzorem 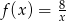 . Zbiór
. Zbiór 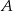 jest zbiorem wszystkich liczb całkowitych
jest zbiorem wszystkich liczb całkowitych  takich, że
takich, że 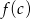 jest liczbą całkowitą. Zatem liczba elementów zbioru
jest liczbą całkowitą. Zatem liczba elementów zbioru 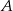 jest równa
jest równa
A) 2 B) 6 C) 8 D) 4
Suma współczynników wielomianu 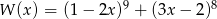 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 3 B) 1 C) 2 D) 0
Na rysunku 1 jest przedstawiony wykres funkcji 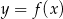 .
.
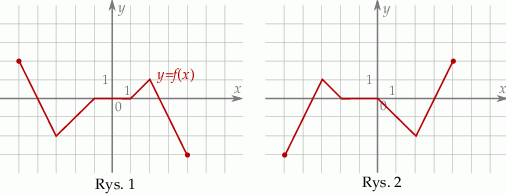
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 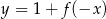 B)
B) 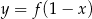 C)
C) 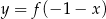 D)
D) 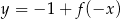
Stosunek pól dwóch kół jest równy 9. Wynika stąd, że promień większego koła jest większy od promienia mniejszego koła
A) 3 razy B) o 9 C) 9 razy D) o 3
Miara kąta  wynosi
wynosi
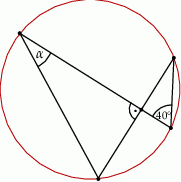
A) 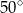 B)
B) 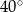 C)
C) 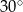 D)
D) 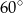
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 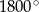 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 12 D) 10
Przez wierzchołek 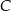 trójkąta prostokątnego
trójkąta prostokątnego 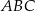 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
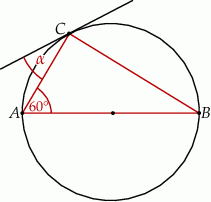
Jeżeli 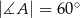 to miara kąta
to miara kąta  jest równa
jest równa
A) 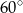 B)
B) 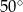 C)
C) 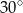 D)
D) 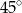
Wysokość trójkąta równobocznego jest o 2 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 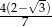 B)
B) 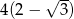 C)
C) 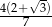 D)
D) 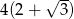
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 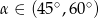 B)
B) 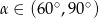 C)
C) 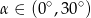 D)
D) 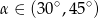
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 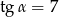 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 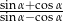 jest równa
jest równa
A)  B)
B)  C)
C)  D)
D) 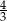
Proste 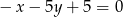 i
i 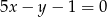 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 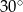 B)
B) 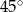 C)
C) 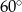 D)
D) 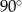
Nierówność 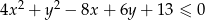 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) zbiór pusty B) punkt C) okrąg D) koło
Środek 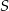 okręgu o równaniu
okręgu o równaniu 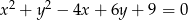 ma współrzędne
ma współrzędne
A) 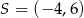 B)
B) 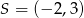 C)
C) 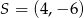 D)
D) 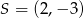
Dany jest ciąg 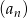 jest określony wzorem
jest określony wzorem 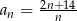 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 5 D) 4
Ciąg 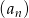 określony jest wzorem
określony jest wzorem 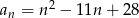 , gdzie
, gdzie 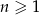 . Liczba niedodatnich wyrazów tego ciągu jest równa
. Liczba niedodatnich wyrazów tego ciągu jest równa
A) 2 B) 7 C) 3 D) 4
Suma początkowych wyrazów ciągu 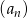 określona jest wzorem
określona jest wzorem 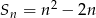 . Piąty wyraz ciągu
. Piąty wyraz ciągu 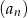 jest równy
jest równy
A) 7 B) 5 C) 23 D) 15
Dane są punkty 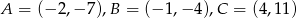 . Wykaż, że punkty te są współliniowe
. Wykaż, że punkty te są współliniowe
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 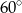 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
Funkcja liniowa 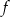 określona jest wzorem
określona jest wzorem 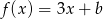 , dla
, dla 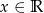 . Wyznacz współczynnik
. Wyznacz współczynnik 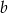 , wiedząc, że
, wiedząc, że 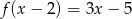 .
.
W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór 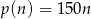 , gdzie
, gdzie  oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność
oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność 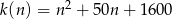 .
.
- Napisz wzór funkcji
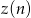 - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
- zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji. - Przy jakiej wielkości produkcji zysk wynosi 0?
- Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?
W dziewięciowyrazowym ciągu arytmetycznym, o pierwszym wyrazie równym 4, wyraz pierwszy, trzeci i siódmy tworzą ciąg geometryczny. Oblicz sumę wyrazów tego ciągu arytmetycznego

