Zestaw użytkownika nr 8038_3581
Sprawdzian funkcja liniowa gr BSuma punktów: 22
Wskaż 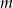 , dla którego funkcja liniowa
, dla którego funkcja liniowa 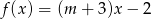 jest malejąca
jest malejąca
A) 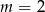 B)
B) 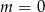 C)
C) 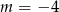 D)
D) 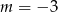
Funkcje 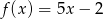 i
i 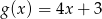 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 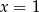 B)
B) 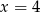 C)
C) 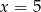 D)
D) 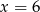
Dana jest funkcja liniowa określona wzorem 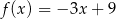 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 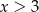 B)
B) 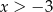 C)
C) 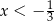 D)
D) 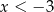
Funkcją malejącą jest funkcja
A) 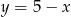 B)
B) 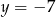 C)
C) 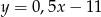 D)
D) 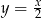
Wykres funkcji liniowej 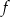 jest prostopadły do prostej
jest prostopadły do prostej 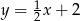 i przechodzi przez punkt
i przechodzi przez punkt 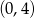 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 2 B) -8 C) 1 D) -1
Wykresem funkcji 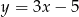 jest prosta równoległa do wykresu funkcji
jest prosta równoległa do wykresu funkcji
A) 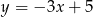 B)
B) 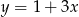 C)
C) 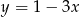 D)
D) 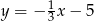
Rozwiąż równanie 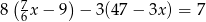 .
.
Rozwiąż nierówność 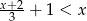 .
.
Rozwiąż algebraicznie i graficznie układ równań 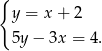
Dla jakich współczynników  i
i  układ
układ 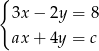
- ma nieskończenie wiele rozwiązań;
- jest sprzeczny?
W układzie współrzędnych zaznacz rozwiązanie układu nierówności 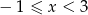 i
i 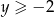 .
.
W hurtowni owoców zmagazynowano 15 ton jabłek. Codziennie hurtownia sprzedaje 120kg jabłek.
- Napisz wzór wyrażający zależność między ilością jabłek pozostających w hurtowni a liczbą dni sprzedaży.
- Określ dziedzinę otrzymanej funkcji.
- Podaj na ile dni sprzedaży wystarczy zgromadzonych jabłek.

