Zestaw użytkownika nr 8062_4307

Rachunek prawdopodobieństwapoziom rozszerzony

Zadanie 1

Uzasadnij, że

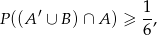
1 P ((A′ ∪ B) ∩ A) ≥ -, 6

jeżeli 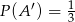′ 1 P(A ) = 3 i ′ 1 P(B ) = 2 .

Zadanie 2

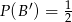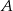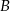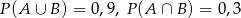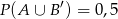O zdarzeniach losowych i wiadomo, że P (A ∪ B) = 0,9, P (A ∩ B ) = 0,3 i P (A ∪ B ′) = 0 ,5 . Oblicz P (A ′ ∪ B ) .

Zadanie 3

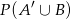Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.

Zadanie 4

Na jednej kostce sześciennej znajdują się liczby: 2,3,3,6,6,6, a na drugiej: 1,1,4,6,7,7. Gra polega na rzucie wybraną kostką. Wygrywa ten, kto wyrzuci większą liczbę na swojej kostce. Masz prawo wyboru kostki. Którą kostkę należy wybrać, aby mieć większe szanse wygranej?

Zadanie 5

Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa następujących zdarzeń:

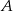– na każdej kostce wypadnie nieparzysta liczba oczek,
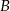– suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.

Zadanie 6

Oblicz prawdopodobieństwo tego, że przy czterokrotnym rzucie kostką, 3 kolejne wyniki utworzą ciąg geometryczny.

Zadanie 7

Do woreczka wrzucono 3 monety 5 złotowe, 4 monety 2 złotowe, 2 monety 1 złotowe oraz 8 monet 50 groszowych. Karol losowo wyjmuje z woreczka 10 monet. Jakie jest prawdopodobieństwo, że wylosuje w ten sposób co najmniej 10 zł? Wynik podaj z dokładnością do trzech miejsc po przecinku.

Zadanie 8

Liczby kul białych, niebieskich i czerwonych tworzą - w podanej kolejności - ciąg arytmetyczny o różnicy 2. Spośród tych kul losujemy jednocześnie trzy. Prawdopodobieństwo wylosowania trzech kul, z których każda jest innego koloru wynosi 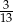3- 13 . Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.

Zadanie 9

W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi 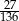21736 . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.

Zadanie 10

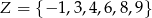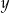Ze zbioru Z = { − 1,3,4,6,8,9} losujemy bez zwracania liczby i . Oblicz prawdopodobieństwa zdarzeń: 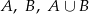A , B, A ∪ B jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 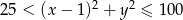25 < (x − 1)2 + y2 ≤ 100 .

Arkusz Wersja PDF