Zestaw użytkownika nr 8126_1403
kąty w kole
Miara kąta  wynosi
wynosi
A) 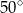 B)
B) 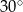 C)
C) 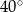 D)
D) 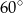
Miara kąta  wynosi
wynosi
A) 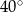 B)
B) 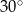 C)
C) 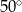 D)
D) 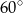
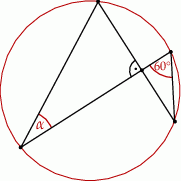
Punkty 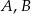 i
i 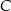 leżą na okręgu o środku
leżą na okręgu o środku 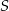 (zobacz rysunek).
(zobacz rysunek).
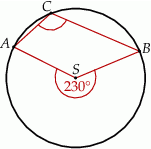
Miara zaznaczonego kąta wpisanego 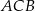 jest równa
jest równa
A) 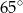 B)
B) 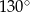 C)
C) 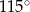 D)
D) 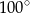
Punkty 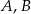 i
i 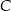 leżą na okręgu o środku
leżą na okręgu o środku 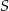 (zobacz rysunek).
(zobacz rysunek).
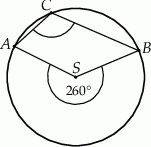
Miara zaznaczonego kąta wpisanego 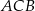 jest równa
jest równa
A) 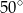 B)
B) 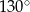 C)
C) 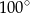 D)
D) 
Punkty 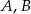 i
i 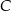 leżą na okręgu o środku
leżą na okręgu o środku 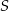 (zobacz rysunek).
(zobacz rysunek).
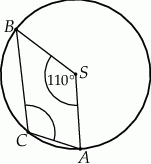
Miara zaznaczonego kąta wpisanego 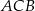 jest równa
jest równa
A) 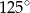 B)
B) 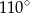 C)
C) 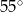 D)
D) 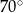
Punkt 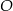 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
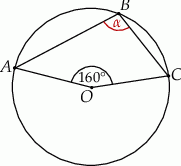
A) 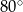 B)
B) 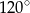 C)
C) 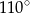 D)
D) 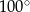
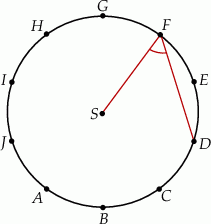
Punkt 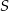 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
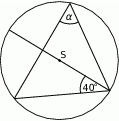
A) 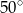 B)
B) 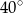 C)
C) 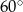 D)
D) 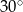
Miara kąta  , zaznaczonego na rysunku, jest równa
, zaznaczonego na rysunku, jest równa
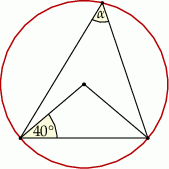
A) 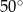 B)
B) 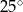 C)
C) 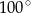 D)
D) 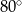
Bok 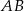 czworokąta
czworokąta  wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 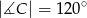 .
.
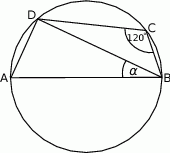
Zatem kąt  ma miarę
ma miarę
A) 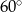 B)
B) 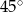 C)
C) 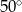 D)
D) 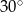
Bok 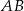 czworokąta
czworokąta 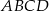 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 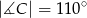 .
.
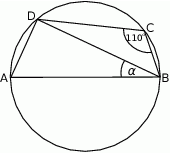
Zatem kąt  ma miarę
ma miarę
A) 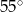 B)
B) 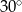 C)
C) 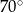 D)
D) 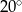
Zaznaczony na rysunku kąt  jest równy
jest równy
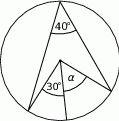
A) 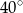 B)
B) 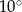 C)
C) 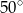 D)
D) 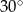
Zaznaczony na rysunku kąt  jest równy
jest równy
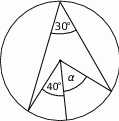
A) 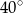 B)
B) 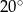 C)
C) 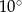 D)
D) 
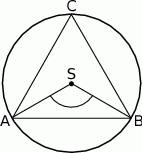
Punkty 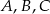 leżące na okręgu o środku
leżące na okręgu o środku 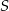 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 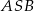 jest równa
jest równa
A) 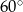 B)
B) 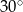 C)
C) 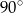 D)
D) 
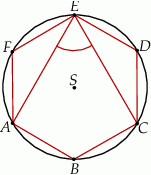
Punkty 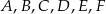 leżące na okręgu o środku
leżące na okręgu o środku 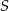 są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 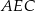 jest równa
jest równa
A) 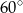 B)
B) 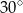 C)
C) 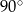 D)
D) 
Jaką miarę ma kąt  ?
?
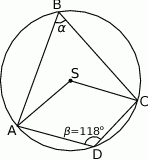
A) 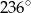 B)
B) 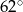 C)
C) 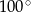 D)
D) 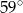
Punkty 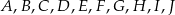 dzielą okrąg o środku
dzielą okrąg o środku 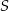 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta  zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 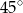 B)
B) 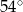 C)
C) 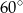 D)
D) 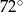
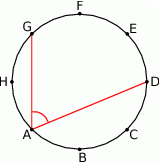
Punkty 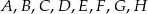 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 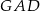 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 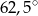 B)
B) 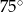 C)
C) 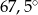 D)
D) 
Punkty 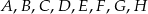 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 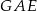 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
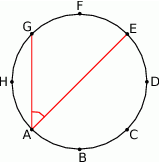
A) 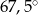 B)
B) 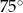 C)
C) 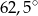 D)
D) 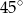
Punkty 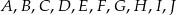 dzielą okrąg o środku
dzielą okrąg o środku 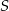 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 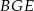 zaznaczonego na rysunku.
zaznaczonego na rysunku.
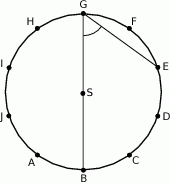
A) 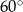 B)
B) 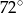 C)
C) 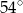 D)
D) 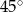
Punkty 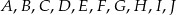 dzielą okrąg o środku
dzielą okrąg o środku 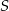 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 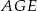 zaznaczonego na rysunku.
zaznaczonego na rysunku.
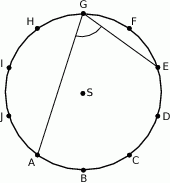
A) 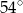 B)
B) 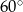 C)
C) 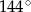 D)
D) 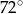
Przez wierzchołek 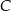 trójkąta prostokątnego
trójkąta prostokątnego 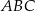 poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie.
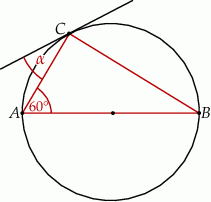
Jeżeli 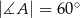 to miara kąta
to miara kąta  jest równa
jest równa
A) 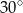 B)
B) 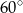 C)
C) 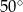 D)
D) 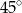
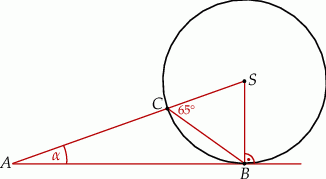
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 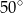 B)
B) 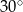 C)
C) 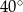 D)
D) 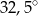
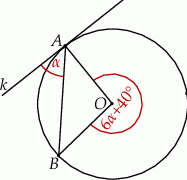
Okrąg o środku 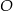 jest styczny do prostej
jest styczny do prostej 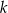 w punkcie
w punkcie 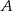 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 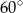 B)
B) 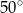 C)
C) 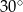 D)
D) 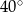
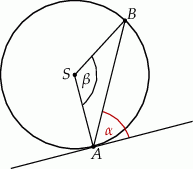
Kąt między cięciwą 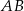 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 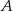 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 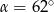 . Wówczas
. Wówczas
A) 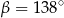 B)
B) 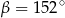 C)
C) 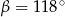 D)
D) 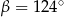
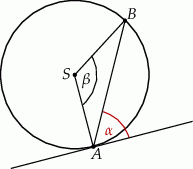
Kąt między cięciwą 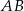 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 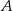 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 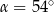 . Wówczas
. Wówczas
A) 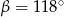 B)
B) 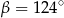 C)
C) 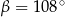 D)
D) 
Na rysunku prosta 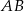 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 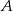 . Punkt
. Punkt 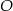 jest środkiem okręgu.
jest środkiem okręgu.
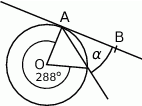
Kąt dopisany  ma miarę:
ma miarę:
A) 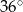 B)
B) 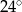 C)
C) 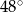 D)
D) 
Na rysunku prosta 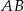 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 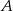 . Punkt
. Punkt 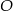 jest środkiem okręgu.
jest środkiem okręgu.
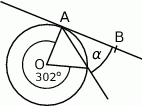
Kąt dopisany  ma miarę:
ma miarę:
A) 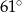 B)
B) 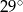 C)
C) 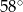 D)
D) 
Na rysunku prosta 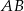 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 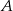 . Punkt
. Punkt 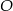 jest środkiem okręgu.
jest środkiem okręgu.
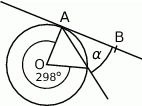
Kąt dopisany  ma miarę:
ma miarę:
A) 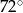 B)
B) 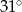 C)
C) 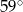 D)
D) 
Prosta 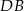 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 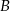 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 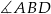 jeśli
jeśli 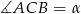 .
.
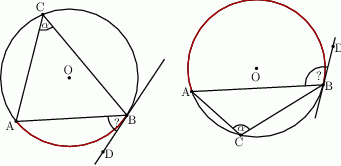
Udowodnij, że jeżeli 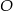 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 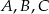 , to
, to 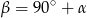 .
.
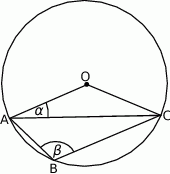
Wiedząc, że punkt 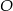 jest środkiem okręgu, oblicz miarę kąta
jest środkiem okręgu, oblicz miarę kąta  .
.
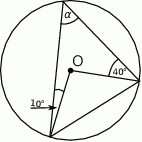
Punkty 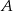 i
i 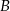 leżą na okręgu o środku
leżą na okręgu o środku 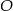 i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
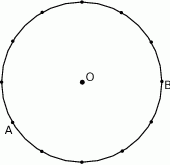
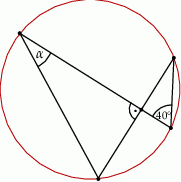
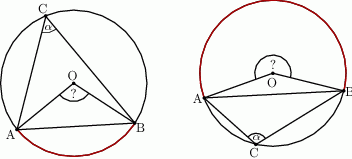
Oblicz miary kątów środkowych 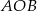 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 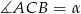 .
.
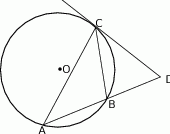
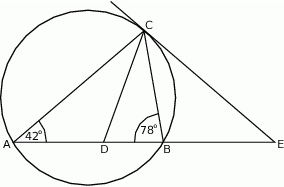
Odcinek 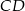 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 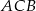 trójkąta
trójkąta 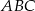 . Kąty trójkąta
. Kąty trójkąta 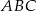 mają miary
mają miary 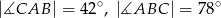 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 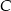 przecina prostą
przecina prostą 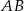 w punkcie
w punkcie 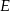 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta 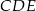 .
.
Prosta 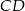 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 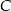 . Uzasadnij, że jeśli
. Uzasadnij, że jeśli 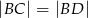 , to
, to 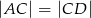 .
.