Zestaw użytkownika nr 8140_6887

Zestaw użytkownika
nr 8140_6887

Zadanie 1

Wazon ma kształt sześcianu, w którym wydrążony jest walec w taki sposób, że styczne górnej podstawy walca, równoległe do odpowiednich krawędzi górnej podstawy sześcianu, są odległe o 1 cm od tych krawędzi; natomiast odległość między dolną podstawą walca, a dolną podstawą sześcianu (grubość dna) jest równa 2 cm.

PIC

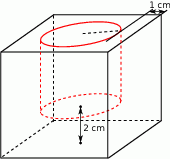
Wiedząc, że stosunek objętości walca do objętości sześcianu jest równy 272π56 , oblicz

  • długość krawędzi sześcianu;
  • objętość walca;
  • do jakiej wysokości wazonu (licząc od dolnej podstawy walca) będzie sięgać poziom wody, jeśli wlejemy do wazonu 125 ml wody. Wynik podaj z dokładnością do 1 mm.
Zadanie 2

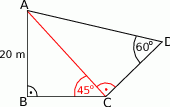
Pan Piotrek ma działkę w kształcie czworokąta, jak na rysunku. Oblicz powierzchnię tej działki. Wynik zaokrąglij do 1 m.

PIC

Zadanie 3

Puszki z napojami chłodzącymi pakuje się w ramach promocji do kartonowych pudełek w kształcie walca. Średnica zewnętrzna puszki wynosi 8 cm, a jej wysokość 15 cm. Jaka jest minimalna objętość pudełka zawierającego cztery puszki? Wynik podaj z dokładnością do 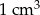1 cm 3 .

PIC

Zadanie 4

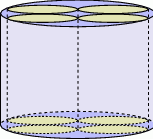
Objętość graniastosłupa prawidłowego trójkątnego jest równa 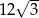√ -- 12 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 36. Oblicz sinus kąta, jaki tworzy przekątna ściany bocznej z sąsiednią ścianą boczną.

Zadanie 5

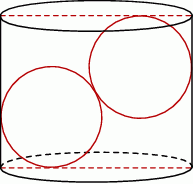
W pojemniku o kształcie walca o promieniu podstawy 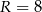R = 8 umieszczono dwie kule o promieniu 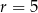r = 5 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.

PIC

Zadanie 6

Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna o długości 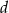d tworzy z wysokością kąt o mierze α .

  • Wyprowadź wzór na objętość walca.
  • Oblicz tę objętość dla 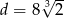d = 8 3√ 2 i α = 60 ∘ .
Zadanie 7

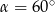Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 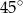45 ∘ obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.

Zadanie 8

Podstawą graniastosłupa prostego jest trójkąt prostokątny równoramienny. Kąt między przekątnymi, wychodzącymi z tego samego wierzchołka, dwóch prostopadłych ścian bocznych, ma miarę 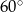60 ∘ . Wiedząc, że objętość tego graniastosłupa jest równa 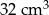32 cm 3 , oblicz pole powierzchni całkowitej tej bryły.

Zadanie 9

Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, z których żadne dwie nie leżą w jednej płaszczyźnie, i otrzymano trójkąt 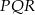PQR

  • Oblicz długości boków trójkąta P QR .
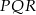  • Wyznacz miary kątów trójkąta P QR .
Zadanie 10

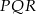W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 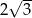√ -- 2 3 . Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem 45 ∘ .

Zadanie 11

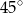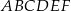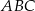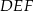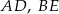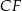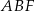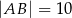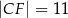Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych AD , BE i CF . Oblicz pole trójkąta ABF wiedząc, że |AB | = 10 i |CF | = 11 . Narysuj ten graniastosłup i zaznacz na nim trójkąt ABF .

Zadanie 12

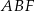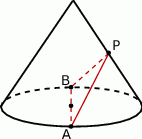
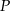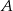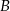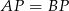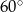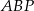Środek P tworzącej stożka połączono z końcami A i B średnicy koła w podstawie stożka tak, że AP = BP . Wiedząc, że kąt rozwarcia stożka jest równy 6 0∘ , oblicz kąty trójkąta ABP .

PIC

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze