Zadanie nr 8271275
Olejarnia wytwarza olej ekologiczny. Aby produkcja była opłacalna, dzienna wielkość produkcji musi wynosić co najmniej 480 litrów i nie może przekroczyć 530 litrów (ze względu na ograniczone moce produkcyjne). Przy poziomie produkcji 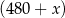 litrów dziennie przeciętny koszt
litrów dziennie przeciętny koszt 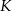 (w złotych) wytworzenia jednego litra oleju jest równy
(w złotych) wytworzenia jednego litra oleju jest równy
![22x 2 − 62 1,5x + 23430 K(x ) = -----------------------, gdzie x ∈ [0,50] 480+ x](https://img.zadania.info/zad/8271275/HzadT2x.gif)
Oblicz, ile litrów oleju dziennie powinna wytworzyć olejarnia, aby przeciętny koszt produkcji jednego litra oleju był najmniejszy (z zachowaniem opłacalności produkcji). Oblicz ten najmniejszy przeciętny koszt.
Rozwiązanie
Musimy zrozumieć przebieg zmienności funkcji
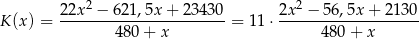
na danym przedziale – w tym celu liczymy pochodną tej funkcji.
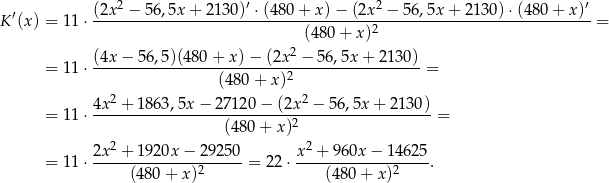
Rozkładamy jeszcze trójmian w liczniku.
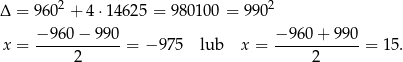
Zatem
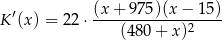
i widzimy, że pochodna jest ujemna w przedziale 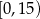 i dodatnia w przedziale
i dodatnia w przedziale ![(1 5,50]](https://img.zadania.info/zad/8271275/HzadR5x.gif) . To oznacza, że funkcja
. To oznacza, że funkcja 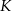 maleje w przedziale
maleje w przedziale ![[0,15]](https://img.zadania.info/zad/8271275/HzadR7x.gif) i rośnie w przedziale
i rośnie w przedziale ![[15,50]](https://img.zadania.info/zad/8271275/HzadR8x.gif) . W takim razie najmniejszy koszt otrzymamy dla
. W takim razie najmniejszy koszt otrzymamy dla 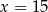 . Mamy wtedy
. Mamy wtedy
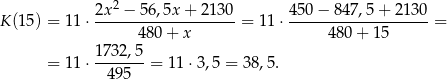
Odpowiedź: