Zestaw użytkownika nr 8360_4267
Matura PróbnarozszerzenieSuma punktów: 50
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 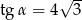 oblicz wartość wyrażenia
oblicz wartość wyrażenia 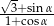 .
.
Wielomian 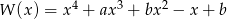 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 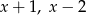 i
i 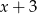 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 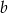 .
.
Wyznacz wzór funkcji 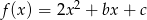 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 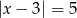 .
.
Rozwiąż nierówność 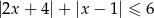 .
.
Rozwiąż nierówność 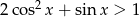 , gdzie
, gdzie 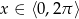 .
.
Rozwiąż układ równań 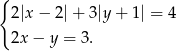
Wyznacz wszystkie wartości parametru 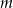 , dla których równanie
, dla których równanie 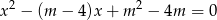 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 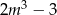 .
.
Punkt 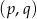 należy do zbioru
należy do zbioru 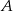 wtedy i tylko wtedy, gdy równanie
wtedy i tylko wtedy, gdy równanie 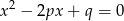 ma dwa różne rozwiązania
ma dwa różne rozwiązania 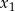 i
i 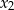 takie, że
takie, że 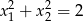 . Zaznacz w układzie współrzędnych zbiór
. Zaznacz w układzie współrzędnych zbiór 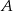 .
.
Rozwiąż równanie 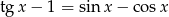 .
.
Dane są funkcje 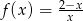 i
i 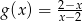 .
.
- Naszkicuj wykresy obu funkcji w jednym układzie współrzędnych.
- Określ przedziały monotoniczności obu funkcji.
- Podaj zbiór rozwiązań nierówności
 .
.

