Zestaw użytkownika nr 8556_8987
Zestaw użytkownika
nr 8556_8987
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Dany jest ciąg arytmetyczny 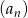 dla
dla 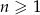 , w którym
, w którym 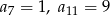 .
.
- Oblicz pierwszy wyraz
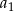 i różnicę
i różnicę  ciągu
ciągu 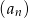 .
. - Sprawdź, czy ciąg
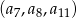 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 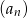 miała wartość najmniejszą.
miała wartość najmniejszą.
Znajdź  , dla którego liczby
, dla którego liczby 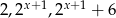 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 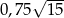 .
.
Dany jest ciąg 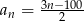 .
.
- Oblicz piętnasty wyraz tego ciągu.
- Którym wyrazem tego ciągu jest liczba 10.
- Ile wyrazów ujemnych ma ten ciąg?
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 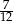 .
.
W ciągu arytmetycznym 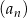 dane są wyrazy:
dane są wyrazy: 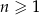 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 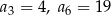 , dla których wyrazy ciągu
, dla których wyrazy ciągu  są mniejsze od 200.
są mniejsze od 200.
Dany jest rosnący ciąg geometryczny 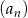 dla
dla 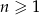 , w którym
, w którym 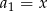 ,
, 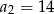 ,
, 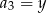 . Oblicz
. Oblicz  oraz
oraz 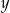 , jeżeli wiadomo, że
, jeżeli wiadomo, że 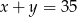 .
.
Ciąg 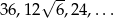 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
- Oblicz iloraz
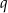 tego ciągu.
tego ciągu. - Zapisz
 -ty wyraz tego ciągu w postaci
-ty wyraz tego ciągu w postaci 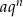
- Oblicz sumę ośmiu początkowych wyrazów tego ciągu.
Liczby 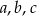 są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby
są trzema kolejnymi wyrazami ciągu arytmetycznego, a liczby 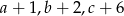 – trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby
– trzema kolejnymi wyrazami ciągu geometrycznego. Znajdź liczby 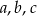 wiedząc, że ich suma jest równa 12.
wiedząc, że ich suma jest równa 12.
Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.

