Zestaw użytkownika nr 8574_8105
Sprawdzian - fakultet gr AFunkcjegr ACzas pracy: 45 min.Suma punktów: 20
Wskaż 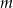 , dla którego funkcja liniowa
, dla którego funkcja liniowa 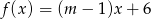 jest rosnąca
jest rosnąca
A) 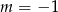 B)
B) 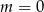 C)
C) 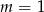 D)
D) 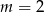
Dana jest funkcja liniowa określona wzorem 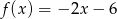 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 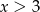 B)
B) 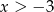 C)
C) 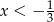 D)
D) 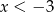
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 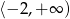 .
.
A) 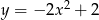 B)
B) 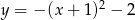 C)
C) 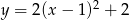 D)
D) 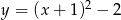
Największą wartością funkcji kwadratowej 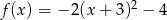 jest
jest
A) 3 B) -2 C) -4 D) 4
Funkcja 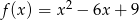 dla argumentu
dla argumentu 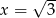 przyjmuje wartość
przyjmuje wartość
A) 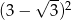 B) -36 C)
B) -36 C) 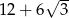 D)
D) 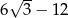
Funkcja 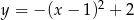 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 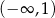 B)
B) 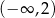 C)
C) 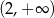 D)
D) 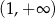
Jeżeli miejscami zerowymi funkcji kwadratowej są liczby 6 oraz -2, a wierzchołek paraboli będącej jej wykresem ma współrzędne 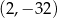 , to wzór tej funkcji można zapisać w postaci
, to wzór tej funkcji można zapisać w postaci
A) 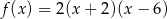
B) 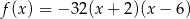
C) 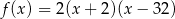
D) 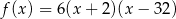
Funkcja 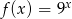 dla argumentu
dla argumentu 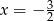 przyjmuje wartość
przyjmuje wartość
A) 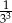 B) 27 C)
B) 27 C) 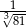 D)
D) 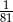
Wskaż zbiór, w którym funkcja 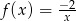 jest rosnąca.
jest rosnąca.
A) 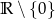 B)
B) 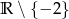 C)
C) 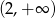 D)
D) 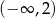
Dziedziną funkcji 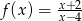 jest zbiór:
jest zbiór:
A) 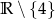 B)
B) 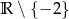 C)
C) 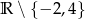 D)
D) 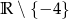
Miejscem zerowym funkcji
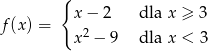
jest liczba
A) -3 B) 3 C) 2 D) 9
Pierwiastkami trójmianu kwadratowego 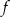 o współczynniku -3 przy najwyższej potędze są liczby
o współczynniku -3 przy najwyższej potędze są liczby 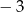 . Oblicz
. Oblicz 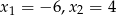 .
.
Poniżej znajduje się fragment wykresu funkcji 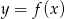 .
.
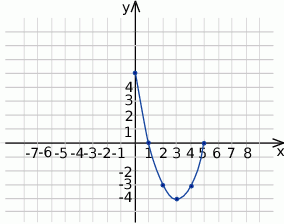
Dorysuj brakującą część wykresu wiedząc, że dziedziną funkcji 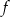 jest przedział
jest przedział 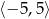 , a wykres jest symetryczny względem osi
, a wykres jest symetryczny względem osi 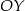 . Następnie na podstawie wykresu funkcji
. Następnie na podstawie wykresu funkcji 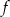 :
:
- podaj, dla jakiego argumentu funkcja przyjmuje najmniejszą wartość;
- oblicz wartość wyrażenia
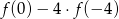 ;
; - podaj liczbę rozwiązań równania
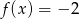 .
.
Przedsiębiorstwo oszacowało, że koszt uruchomienia produkcji lamp nowego typu wyniesie 15 600 zł, a koszt pojedynczej lampy wyniesie 80 zł. Niech  oznacza liczbę wyprodukowanych lamp.
oznacza liczbę wyprodukowanych lamp.
- Wyraź całkowity koszt produkcji lamp jako funkcję argumentu
 .
. - Wyraź całkowity zysk jako funkcję argumentu
 , jeżeli przedsiębiorstwo sprzedaje hurtowniom lampy po 100 zł za sztukę.
, jeżeli przedsiębiorstwo sprzedaje hurtowniom lampy po 100 zł za sztukę. - Ile sztuk sprzedanych lamp zwróci koszty uruchomienia ich produkcji.

