Zestaw użytkownika nr 8590_8781
Zestaw użytkownika
nr 8590_8781
Wykaż, że jeżeli 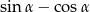 jest liczbą wymierną to wymierna jest również liczba
jest liczbą wymierną to wymierna jest również liczba 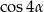 .
.
Wyznacz największą wartość funkcji
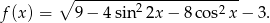
Wyznacz zbiór wartości funkcji: 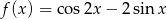 , gdzie
, gdzie 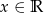 .
.
Wyznacz zbiór wartości funkcji
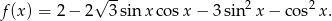
Wyznacz zbiór wartości funkcji
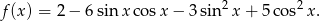
Oblicz możliwe wartości wyrażenia 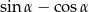 wiedząc, że
wiedząc, że 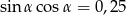 .
.
Posługując się wykresem funkcji 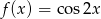 dla
dla 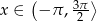 , rozwiąż nierówność
, rozwiąż nierówność 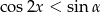 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 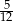 okręgu.
okręgu.
Rozwiąż nierówność 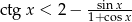 , gdzie
, gdzie 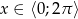 ;
;
Rozwiąż nierówność 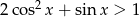 , gdzie
, gdzie 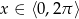 .
.
Rozwiąż nierówność 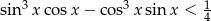 , gdzie
, gdzie 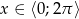 .
.
Rozwiąż nierówność 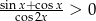 , gdzie
, gdzie 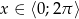 .
.
Rozwiąż nierówność 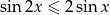 .
.
Rozwiąż nierówność: 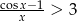 dla
dla 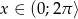 .
.
Rozwiąż równanie 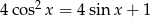 w przedziale
w przedziale 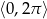 .
.
Dla jakich wartości parametru 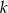 równanie
równanie 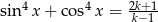 ma rozwiązanie?
ma rozwiązanie?
Dla jakich wartości parametru 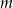 równanie
równanie 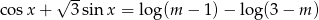 ma rozwiązania.
ma rozwiązania.
Rozwiąż równanie 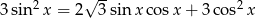 w przedziale
w przedziale 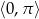 .
.
Rozwiąż równanie 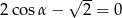 , gdy
, gdy 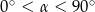 .
.
Rozwiąż równanie 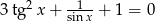 .
.
Rozwiąż równanie: 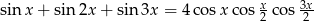 .
.
Wyznacz wszystkie rozwiązania równania 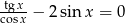 .
.
Dana jest funkcja 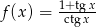 dla
dla 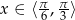 .
.
- Rozwiąż równanie
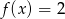 .
. - Wyznacz najmniejszą wartość funkcji
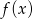 .
.
Rozwiąż równanie 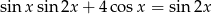
Rozwiąż równanie 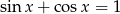 .
.
Rozwiąż równanie 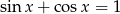 .
.
Rozwiąż równanie 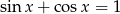 .
.
Rozwiąż równanie 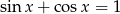 .
.
Rozwiąż równanie 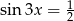 .
.
Rozwiąż równanie 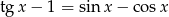 .
.
Wyznacz zbiór wartości parametru 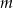 , dla których równanie:
, dla których równanie: 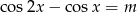 ma rozwiązania.
ma rozwiązania.
Dana jest funkcja 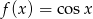 . Rozwiąż równanie
. Rozwiąż równanie 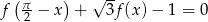 .
.
Rozwiąż równanie 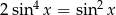 .
.
Rozwiąż równanie 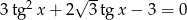 .
.
Rozwiąż równanie 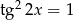 .
.
Dla jakich wartości parametru 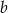 istnieje kąt
istnieje kąt  taki, że
taki, że 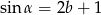 ?
?
Rozwiąż równanie 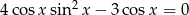 .
.
Rozwiąż równanie 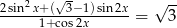 .
.
Rozwiąż równanie 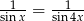 w przedziale
w przedziale 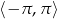 .
.
Oblicz sumę stu najmniejszych dodatnich rozwiązań równania 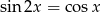 .
.
Rozwiąż równanie 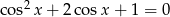 .
.

