Zestaw użytkownika nr 8593_7840
Zestaw użytkownika
nr 8593_7840
Rozwiąż równanie 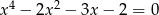 .
.
Rozwiąż równanie 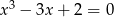 .
.
Rozwiąż równanie 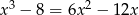 .
.
Rozwiąż równanie 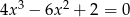 .
.
Rozwiąż równanie 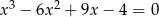 .
.
Rozwiąż równanie 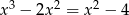 .
.
Rozwiąż nierówność 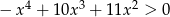 .
.
Rozwiąż nierówność 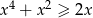 .
.
Wyznacz wszystkie wartości 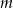 , dla których nierówność
, dla których nierówność 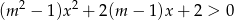 jest prawdziwa dla każdego
jest prawdziwa dla każdego 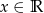 .
.
Wyznacz te wartości parametru 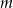 , dla których nierówność
, dla których nierówność 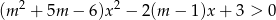 jest prawdziwa dla każdego
jest prawdziwa dla każdego 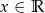 .
.
Wyznacz te wartości parametru 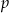 , dla których nierówność
, dla których nierówność 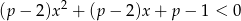 nie ma rozwiązań.
nie ma rozwiązań.
Dla jakich wartości parametru 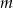 równanie
równanie 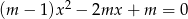 posiada 2 różne rozwiązania?
posiada 2 różne rozwiązania?
Dla jakich wartości parametru 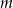 równanie
równanie 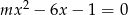 ma co najmniej jedno rozwiązanie?
ma co najmniej jedno rozwiązanie?
Wyznacz te wartości parametru 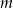 , dla których równanie
, dla których równanie 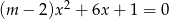 ma jedno rozwiązanie.
ma jedno rozwiązanie.
Dla jakich 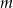 równanie
równanie 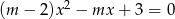 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Określ liczbę pierwiastków równania 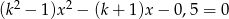 w zależności od wartości parametru
w zależności od wartości parametru 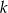 .
.
Wyznacz te wartości parametru 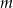 , dla których równanie
, dla których równanie 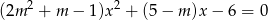 ma dwa różne pierwiastki tego samego znaku.
ma dwa różne pierwiastki tego samego znaku.
Dla jakich wartości parametru 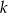 równanie
równanie 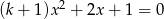 ma dwa rozwiązania przeciwnych znaków.
ma dwa rozwiązania przeciwnych znaków.
Wyznacz te wartości parametru 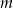 , dla których równanie
, dla których równanie 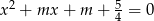 ma dwa różne pierwiastki nieujemne.
ma dwa różne pierwiastki nieujemne.
Dla jakich wartości parametru 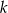 równanie
równanie 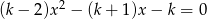 ma tylko ujemne rozwiązania?
ma tylko ujemne rozwiązania?

