Zestaw użytkownika nr 8600_7812
Zestaw użytkownika
nr 8600_7812
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia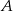 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,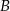 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 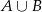 .
.
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
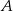 – wszystkie kule znajdą się w szufladach z numerami parzystymi.
– wszystkie kule znajdą się w szufladach z numerami parzystymi. 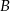 – dokładnie dwie szuflady pozostaną puste.
– dokładnie dwie szuflady pozostaną puste.
Spośród wyrazów skończonego ciągu arytmetycznego 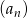 danego wzorem
danego wzorem 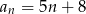 , gdzie
, gdzie 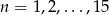 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
Ze zbioru 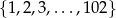 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Dany jest wielomian 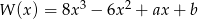 . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
. Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
O zdarzeniach 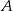 i
i 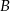 wiadomo, że
wiadomo, że 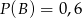 ,
, 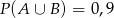 oraz
oraz 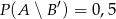 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 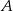 .
.
Dane są zbiory liczb całkowitych: 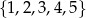 i
i 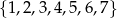 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Każdej karcie bankomatowej jest przypisany numer identyfikacyjny zwany kodem PIN. Kod ten składa się z czterech cyfr (cyfry mogą się powtarzać, ale kodem PIN nie może być 0000). Oblicz prawdopodobieństwo, że w losowo utworzonym kodzie PIN żadna cyfra się nie powtórzy. Wynik podaj w postaci ułamka nieskracalnego.
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 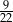 .
.
Niech  będzie liczbą naturalną. Ze zbioru liczb
będzie liczbą naturalną. Ze zbioru liczb 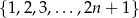 losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od
losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od 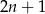 .
.
Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.
W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
Prawdopodobieństwa zdarzeń 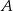 i
i 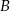 oraz zdarzeń do nich przeciwnych spełniają warunki:
oraz zdarzeń do nich przeciwnych spełniają warunki: 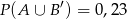 i
i 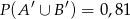 .
.
- Oblicz
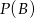 .
. - Wykaż, że jeżeli
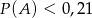 to
to 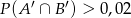 .
.
W urnie znajduję się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.

