Zestaw użytkownika nr 8613_2186
kombinatoryka i p-wo cz.1 podstawa
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 70 D) 28
Pan Jakub ma 8 marynarek, 5 par różnych spodni i 9 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 90 B) 22 C) 360 D) 240
Pan Tomasz ma 5 marynarek, 9 par różnych spodni i 6 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 20 B) 45 C) 270 D) 280
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 22 B) 280 C) 132 D) 264
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste?
A) 20 B) 16 C) 25 D) 24
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których pierwsza cyfra jest parzysta, a druga nieparzysta?
A) 16 B) 25 C) 24 D) 20
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są nieparzyste?
A) 20 B) 16 C) 24 D) 25
Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 80 B) 82 C) 81 D) 90
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 20 B) 25 C) 30 D) 16
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są większe od 4 jest
A) 16 B) 25 C) 20 D) 30
W kolejce do kasy biletowej ustawiły się cztery dziewczynki i pięciu chłopców. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 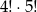 B) 9! C) 4!+5! D)
B) 9! C) 4!+5! D) 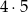
W kolejce do kasy kinowej ustawiło się sześciu mężczyzn i trzy kobiety. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 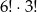 B) 9! C) 6!+3! D)
B) 9! C) 6!+3! D) 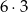
Wybieramy jedną liczbę ze zbioru 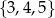 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 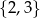 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 4 C) 3 D) 5
Wybieramy jedną liczbę ze zbioru 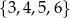 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 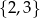 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą parzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą parzystą?
A) 4 B) 5 C) 3 D) 6
Wybieramy jedną liczbę ze zbioru 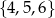 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 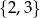 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 5 B) 3 C) 6 D) 4
Wybieramy liczbę  ze zbioru
ze zbioru 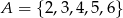 oraz liczbę
oraz liczbę 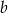 ze zbioru
ze zbioru 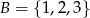 . Ile jest takich par
. Ile jest takich par 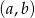 , że iloczyn
, że iloczyn 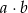 jest liczbą parzystą?
jest liczbą parzystą?
A) 5 B) 9 C) 11 D) 21
W karcie dań jest 5 zup i 4 drugie dania. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 20 B) 25 C) 16 D) 9
Ze zbioru liczb 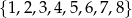 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 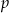 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 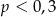 B)
B) 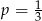 C)
C) 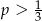 D)
D) 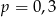
Ze zbioru liczb 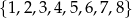 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 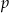 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 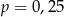 B)
B) 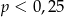 C)
C) 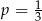 D)
D) 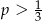
Ze zbioru liczb 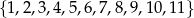 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 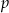 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 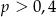 B)
B) 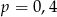 C)
C) 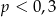 D)
D) 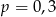
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 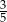 B)
B)  C)
C)  D)
D) 
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 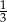 B)
B)  C)
C) 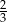 D)
D) 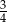
Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B) 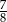 C)
C)  D)
D) 
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 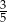 B)
B) 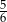 C)
C)  D)
D) 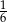
Ze zbioru 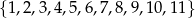 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 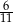 B)
B) 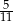 C)
C) 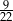 D)
D) 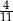
Ze zbioru 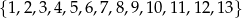 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 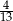 B)
B) 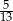 C)
C) 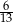 D)
D) 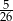
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 9, jest równe
A) 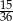 B)
B) 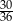 C)
C) 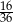 D)
D) 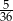
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najmniej 5, jest równe
A) 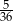 B)
B)  C)
C) 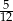 D)
D) 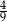
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 10, jest równe
A) 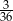 B)
B) 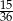 C)
C) 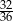 D)
D) 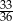
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek podzielnej przez 3 jest równe
A) 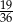 B)
B) 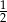 C)
C) 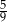 D)
D) 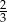
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek większej od 4 jest równe
A) 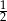 B)
B)  C)
C) 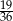 D)
D) 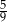
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 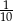 B)
B) 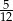 C)
C) 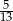 D)
D) 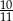
Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadną co najmniej dwa oczka.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że w każdym rzucie otrzymamy inną liczbę oczek.
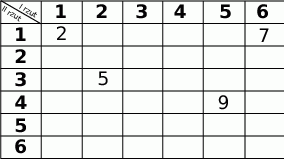
Rzucamy dwa razy symetryczną, sześcienną kostką do gry i zapisujemy sumę liczb wyrzuconych oczek.
- Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia.
- Oblicz prawdopodobieństwo zdarzenia
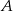 , polegającego na tym, że suma liczb oczek jest liczbą nieparzystą.
, polegającego na tym, że suma liczb oczek jest liczbą nieparzystą. - Oblicz prawdopodobieństwo zdarzenia
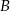 , polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
, polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:
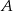 — w każdym rzucie wypadnie nieparzysta liczba oczek.
— w każdym rzucie wypadnie nieparzysta liczba oczek. 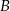 -– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9. 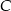 -– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne: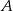 – w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim; – suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na pierwszej kostce wypadło dwa razy mniej oczek niż na drugiej?
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na każdej kostce będzie co najmniej 5 oczek?

