Zestaw użytkownika nr 8677_6635
Sprawdzian funkcja wymierna gr B
Zbiór 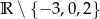 jest dziedziną wyrażenia:
jest dziedziną wyrażenia:
A) 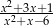 B)
B) 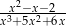 C)
C) 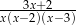 D)
D) 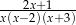
Dziedziną funkcji 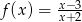 jest zbiór:
jest zbiór:
A) 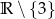 B)
B) 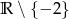 C)
C) 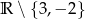 D)
D) 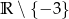
Dziedziną funkcji 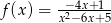 jest zbiór
jest zbiór
A) 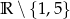 B)
B) 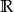 C)
C) 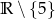 D)
D) 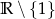
Równanie 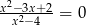 ma:
ma:
A) 2 pierwiastki B) 3 pierwiastki C) 1 pierwiastek D) 4 pierwiastki
Zbiorem rozwiązań nierówności 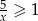 jest przedział
jest przedział
A) 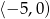 B)
B) 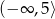 C)
C) 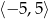 D)
D) 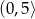
Zbiorem rozwiązań nierówności 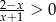 jest
jest
A) 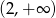 B)
B) 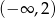 C)
C) 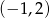 D)
D) 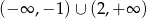
Do wykresu funkcji 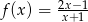 należy punkt
należy punkt
A) 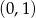 B)
B) 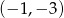 C)
C) 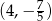 D)
D) 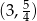
Zbiorem wartości funkcji 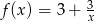 jest
jest
A) 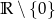 B)
B) 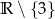 C)
C) 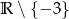 D)
D) 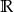
Wykres funkcji 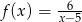 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 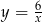 o 5 jednostek
o 5 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Dana jest funkcja 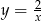 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→u = [1,− 5]](https://img.zadania.info/zad/5948271/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Rozwiąż równanie 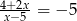 .
.
Wykres funkcji 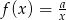 dla
dla 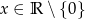 , gdzie
, gdzie 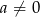 , przesunięto o wektor
, przesunięto o wektor ![→u = [− 3,2]](https://img.zadania.info/zad/2875082/HzadT3x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 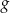 . Do wykresu funkcji
. Do wykresu funkcji 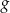 należy punkt
należy punkt 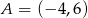 . Oblicz
. Oblicz  , następnie rozwiąż nierówność
, następnie rozwiąż nierówność 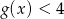 .
.

