Zestaw użytkownika nr 8680_6406
Ciągi liczbowe (poziom podstawowy) A
W ciągu arytmetycznym 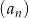 pierwszy wyraz jest równy 45, zaś
pierwszy wyraz jest równy 45, zaś 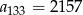 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba
A) 15 B) 13 C) 16 D) 14
Dany jest ciąg arytmetyczny, w którym 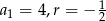 . Wtedy
. Wtedy
A) 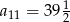 B)
B) 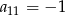 C)
C) 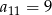 D)
D) 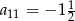
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 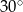 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 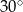 B)
B) 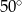 C)
C) 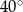 D)
D) 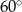
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 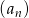 danego wzorem
danego wzorem 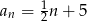 jest równa
jest równa
A) 210 B) 410 C) 205 D) 200
Dany jest ciąg arytmetyczny o pierwszym wyrazie 8 i różnicy 6. Wyraz ogólny ciągu wyraża się wzorem
A) 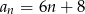 B)
B) 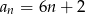 C)
C) 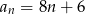 D)
D) 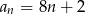
Ciąg arytmetyczny tworzą liczby
A) 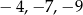 B) -4,-7,-9 C) 3,9,27 D)
B) -4,-7,-9 C) 3,9,27 D) 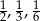
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
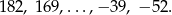
Ile liczb napisano na tablicy?
A) 18 B) 17 C) 19 D) 20
Ciągiem geometrycznym jest ciąg określony wzorem
A) 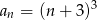 B)
B) 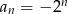 C)
C) 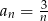 D)
D) 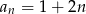
Jeśli trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy 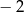 , to drugi wyraz jest równy
, to drugi wyraz jest równy
A) 8 B) -2 C) 2 D) -8
Liczby 9,-3 i 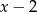 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) 1 B) -1,5 C) 5 D) 3
Dany jest ciąg geometryczny o wyrazie ogólnym 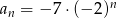 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 56 B) -28 C) -56 D) 28
W ciągu geometrycznym 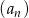 dane są
dane są 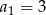 i
i 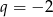 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 257 B) 255 C) -257 D) -255
W dziewięciowyrazowym ciągu arytmetycznym, o pierwszym wyrazie równym 4, wyraz pierwszy, trzeci i siódmy tworzą ciąg geometryczny. Oblicz sumę wyrazów tego ciągu arytmetycznego
Ciąg 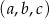 jest arytmetyczny
jest arytmetyczny 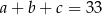 . Ciąg
. Ciąg 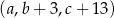 jest geometryczny. Oblicz
jest geometryczny. Oblicz 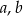 i
i  .
.
Uzasadnij, że ciąg określony wzorem 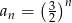 jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.

