Zestaw użytkownika nr 8746_9243
Zestaw użytkownika
nr 8746_9243
Funkcja 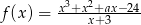 ma miejsce zerowe równe (-2). Wyznacz:
ma miejsce zerowe równe (-2). Wyznacz:
- wartość parametru
 ;
; - pozostałe miejsca zerowe funkcji;
- zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne.
Wyznacz wszystkie wartości parametru 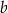 , dla których równanie
, dla których równanie 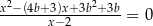 ma dwa rozwiązania różnych znaków.
ma dwa rozwiązania różnych znaków.
Określ liczbę rozwiązań równania 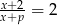 w zależności od wartości parametru
w zależności od wartości parametru 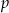 .
.
Określ liczbę rozwiązań równania 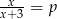 w zależności od wartości parametru
w zależności od wartości parametru 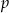 .
.
Jednym z miejsc zerowych funkcji 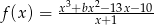 jest 5.
jest 5.
- Znajdź współczynnik
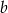 .
. - Znajdź pozostałe miejsca zerowe funkcji
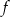 .
. - Wyznacz przedziały monotoniczności funkcji.
Wyznacz te wartości parametru 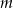 , dla których równanie
, dla których równanie 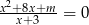 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Wiadomo, że liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 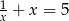 , gdzie
, gdzie 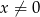 . Nie wyznaczając
. Nie wyznaczając  , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 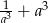 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 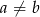 oraz
oraz 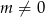 równanie
równanie
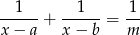
ma dwa różne rozwiązania.
Dane jest równanie 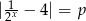 z parametrem
z parametrem 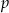 . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 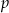 .
.
Dla jakich wartości parametru  równanie
równanie 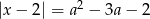 ma dwa pierwiastki różnych znaków?
ma dwa pierwiastki różnych znaków?
Dla jakich wartości parametru 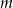 równanie
równanie 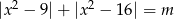 ma dokładnie dwa różne pierwiastki.
ma dokładnie dwa różne pierwiastki.
Dla jakich wartości parametru 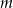 równanie
równanie 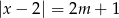 ma jedno rozwiązanie?
ma jedno rozwiązanie?
Rozwiąż algebraicznie układ równań 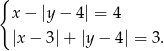
Wyznacz wszystkie wartości parametru 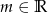 , dla których równanie
, dla których równanie 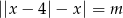 ma tylko jedno rozwiązanie.
ma tylko jedno rozwiązanie.
Wyznacz te wartości parametru 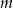 , dla których równanie
, dla których równanie
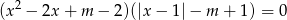
ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki.
Zbadaj liczbę rozwiązań równania 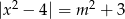 w zależności od parametru
w zależności od parametru 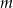 .
.

