Zestaw użytkownika nr 8790_6174
Geometria płaskaTrójkąty, czworokąty, okręgi wpisane i opisane
W trójkącie prostokątnym wysokość poprowadzona na przeciwprostokątną ma długość 10 cm, a promień okręgu opisanego ma długość 19 cm. Oblicz pole tego trójkąta.
Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 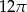 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trapezie kąty przy dłuższej podstawie to 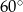 i
i 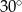 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
Stosunek długości przekątnych rombu o boku 17 cm jest równy 5:3. Oblicz pole rombu.
Dany jest trójkąt prostokątny 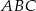 , w którym
, w którym 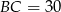 ,
, 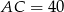 i
i 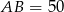 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 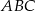 jest styczny do boku
jest styczny do boku 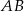 w punkcie
w punkcie 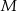 . Oblicz długość odcinka
. Oblicz długość odcinka 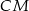 .
.
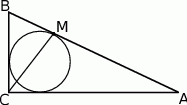
Przyprostokątne trójkąta 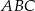 mają długości 10 i 24. Przeciwprostokątna trójkąta
mają długości 10 i 24. Przeciwprostokątna trójkąta 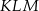 podobnego do niego ma długość 39. Oblicz pole trójkąta
podobnego do niego ma długość 39. Oblicz pole trójkąta 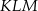 .
.
Dwa krótsze boki trójkąta rozwartokątnego mają długości 5cm i 6cm. Jakie wartości może przyjmować długość trzeciego boku trójkąta?
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 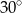 i
i 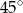 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 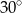 i
i 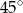 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
W rombie jedna z przekątnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekątnych pole rombu jest większe od 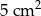 ?
?
Dany jest trapez prostokątny 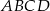 , gdzie
, gdzie 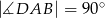 ,
, 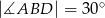 ,
, 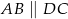 ,
, 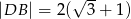 i
i 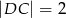 .
.
- Oblicz długość promienia okręgu wpisanego w trójkąt
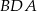 .
. - Wyznacz sumę kwadratów sinusów kątów wewnętrznych trapezu
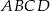 .
.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
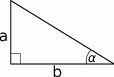
Dany jest trójkąt prostokątny, w którym  ,
, 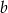 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 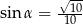 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
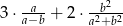 .
.
Odcinki 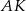 i
i 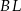 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 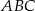 , a punkt
, a punkt 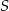 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
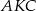 i
i 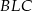 ;
; 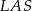 i
i 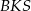 ;
; 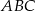 i
i 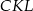 .
.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 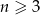 wyraża się wzorem
wyraża się wzorem 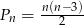 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Kąt ostry między przekątnymi równoległoboku 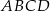 ma miarę
ma miarę 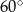 . Przekątna
. Przekątna 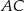 ma długość 6, a przekątna
ma długość 6, a przekątna 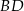 jest prostopadła do boku
jest prostopadła do boku 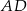 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
W prostokącie połączono środki sąsiednich boków. Powstały w ten sposób romb ma obwód 40 cm i pole równe 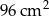 . Oblicz długości boków prostokąta.
. Oblicz długości boków prostokąta.
Krótsza przekątna rombu o długości 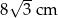 dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
Wyznacz wszystkie wartości  , dla których liczby
, dla których liczby 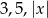 mogą być długościami boków trójkąta.
mogą być długościami boków trójkąta.
W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
Z punktu 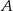 leżącego na okręgu o promieniu
leżącego na okręgu o promieniu 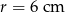 i środku
i środku 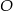 poprowadzono dwie równej długości cięciwy
poprowadzono dwie równej długości cięciwy 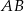 i
i 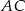 tworzące kąt
tworzące kąt 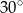 . Oblicz pole czworokąta
. Oblicz pole czworokąta 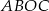 .
.

