Zestaw użytkownika nr 8798_3496
Funkcje-sprawdzian27 Marca 2012Czas pracy: 45 min.Suma punktów: 34
Dane są funkcje liniowe 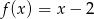 oraz
oraz 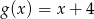 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 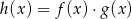 .
.
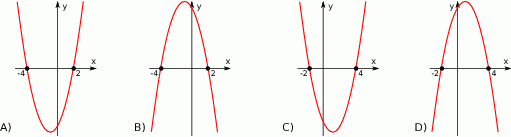
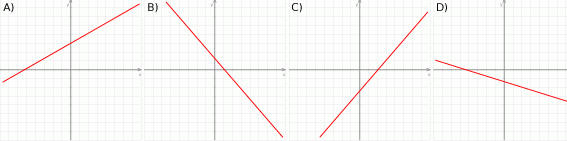
Na którym rysunku przedstawiono wykres funkcji liniowej 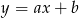 takiej, że
takiej, że 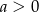 i
i 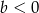 ?
?
Wskaż 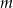 , dla którego funkcja liniowa
, dla którego funkcja liniowa 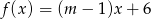 jest rosnąca
jest rosnąca
A) 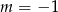 B)
B) 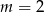 C)
C) 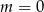 D)
D) 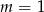
Do wykresu funkcji 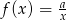 , dla
, dla 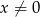 należy punkt
należy punkt 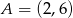 . Wtedy
. Wtedy
A) 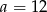 B)
B) 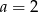 C)
C) 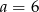 D)
D) 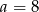
Prosta o równaniu 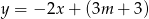 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 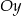 w punkcie
w punkcie 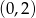 . Wtedy
. Wtedy
A) 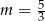 B)
B) 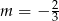 C)
C) 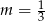 D)
D) 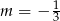
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział 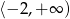 .
.
A) 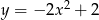 B)
B) 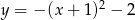 C)
C) 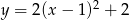 D)
D) 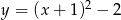
Prosta 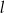 ma równanie
ma równanie 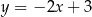 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 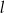 i przechodzącej przez punkt
i przechodzącej przez punkt 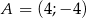 jest:
jest:
A) 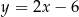 B)
B) 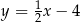 C)
C) 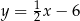 D)
D) 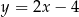
Największą wartością funkcji kwadratowej 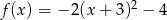 jest
jest
A) -2 B) 4 C) 3 D) -4
Wierzchołek paraboli o równaniu 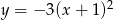 ma współrzędne
ma współrzędne
A) 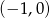 B)
B) 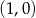 C)
C) 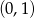 D)
D) 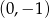
Wierzchołek paraboli 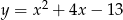 leży na prostej o równaniu
leży na prostej o równaniu
A) 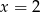 B)
B) 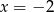 C)
C) 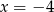 D)
D) 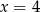
Wykres funkcji kwadratowej 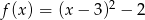 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 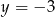 B)
B) 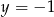 C)
C) 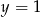 D)
D) 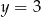
Oblicz największą i najmniejszą wartość funkcji 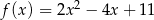 w przedziale
w przedziale 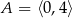 .
.
Na rysunku jest przedstawiony wykres funkcji 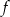 .
.
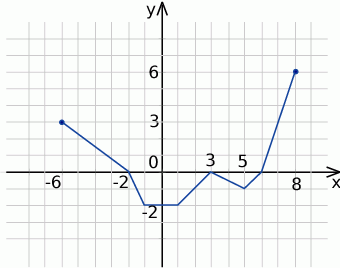
- Podaj dziedzinę funkcji
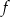 .
. - Podaj wszystkie miejsca zerowe funkcji
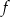 .
. - Odczytaj wartość funkcji
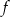 dla argumentu
dla argumentu 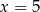 .
. - Podaj zbiór wartości funkcji
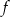 .
. - Podaj maksymalny przedział o długości 3, w którym funkcja
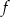 jest rosnąca.
jest rosnąca. - Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja
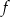 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Napisz wzór funkcji liniowej, której wykres przechodzi przez punkty 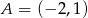 i
i 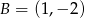 .
.
Funkcja 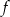 jest określona wzorem
jest określona wzorem
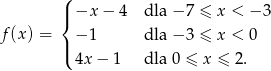
- Podaj dziedzinę funkcji
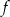 .
. - Podaj jej miejsca zerowe.
- Naszkicuj wykres tej funkcji.
- Podaj zbiór wartości funkcji
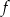 .
.
Dany jest wykres funkcji 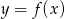 określonej dla
określonej dla 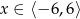 .
.
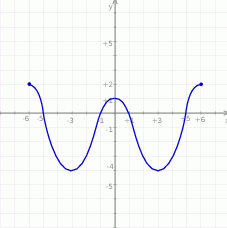
Korzystając z wykresu funkcji zapisz:
- maksymalne przedziały, w których funkcja jest rosnąca;
- zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie;
- największą wartość funkcji
 w przedziale
w przedziale 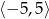 ;
; - miejsca zerowe funkcji
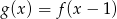 ;
; - najmniejszą wartość funkcji
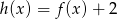 .
.
Podaj wartość wyrażenia 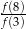 jeżeli
jeżeli 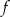 jest funkcją kwadratową o miejscach zerowych 2 i 4.
jest funkcją kwadratową o miejscach zerowych 2 i 4.
Funkcja kwadratowa 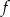 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu -4, a do jej wykresu należy punkt 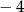 . Napisz wzór funkcji
. Napisz wzór funkcji 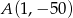 w postaci ogólnej.
w postaci ogólnej.

